Morning lectures

• Andrei Bernevig (Princeton University, EE.UU.)
  
  Topological Superconductors and Category Theory
  
  • Topological Superconductivity, Kitaev wire, p+ip superconductor in 2D and relation to projector Chern numbers, Majorana fermions.
  • Different kinds of chiral superconductors - the 16 fold way
  • Modular tensor categories, braiding,and topological quantum field theory

  
  Andrei's lecture notes
  
• Allan Macdonald (University of Texas at Austin, EE.UU.)
  
  Quantum Hall Effects Through the Ages
  
  • Chern Indices and the Quantum Hall Effect (covers Thouless's original paper)
  • Fractional Quantum Hall Effect (covers incompressible states, fractional and non-Abelian excitations)
  • Quantum Hall Effect in a Periodic Potential (covers Hofstadter butterfly, Chern insulators, QHE for graphene on h-BN)
  • Landau Levels and Superconductivity (covers Hall quantization in the presence of a pair-potential and proximity-coupled superconductivity in graphene sheets with well formed Landau levels)
• Jiannis Pachos (University Leeds, Reino Unido).
  
  Why should anyone care about anyons?
  
  • General overview of anyons and topological systems
  • The toric code and quantum error correction (maybe finite temperature effects)
  • Anyons, Jones polynomials and quantum algorithms
  • Topological entanglement entropy

Short communications

• Aiyama Balachandran (Syracuse University, Syracuse, New York, USA)
  
  Edge states, topological insulators and superconductors
  On manifolds \(M\) with boundaries \(\partial M\), the formulation of quantum field theories for tensor fields requires boundary conditions on the Laplacian \(\Delta\) such as Dirichlet, Neumann or Robin boundary conditions. They can lead to edge states with a gapped bulk. Examples are quantum Hall effect and the interface \(\partial M\) of a superconducting \(M\) and a normal metal. We discuss this phenomenon in general terms, give examples and suggest that they are very common. Such edge states occur for Dirac fields too, but the boundary conditions are those of Atiyah, Pataudi and Singer (APS). The APS approach is explained and shown to lead to edge states by examples. Perhaps these edge states are related to "topological" edge states. They can conserve \(P\) and \(T\) and lead to spin-momentum locking.
  (Bal's presentation)
  
• César Galindo (Universidad de los Andes, Bogotá, Colombia)
  
  Classification of Modular Categories
  Modular categories are intricate organizing algebraic structures appearing in a variety of mathematical subjects including topological quantum field theory, conformal field theory, representation theory of quantum groups, von Neumann algebras, and vertex operator algebras. Besides the mathematical interest, a motivation for a classification of modular categories comes from their application in condensed matter physics and quantum computing. Unitary modular categories are algebraic models of anyons in two dimensional topological phases of matter where simple objects model anyons. In topological quantum computation, anyons give rise to quantum computational models. Modular categories have also been used recently to construct three dimensional topological insulators and superconductors. Therefore, a classification of modular categories is literally a classification of certain topological phases of matter.
  In this talk we will present the classification of all modular categories of dimension \(4m\), where \(m\) is an odd square-free integer. We will use this result to give the classification of rank 6 and rank 7 weakly integral modular categories. This completes the classification of weakly integral modular categories through rank 7.

  This talk is based on a joint work with P. Bruillard, S-H. Ng, J. Plavnik, E. Rowell and Z. Wang (Prepint: arXiv:1411.2313).

  
  (César's presentation)
  
• Arturo Gómez (Departamento de Ciencias, Facultad de Artes Liberales y Facultad de Ingeniería y Ciencias, Universidad Adolfo Ibañez, Viña del Mar, Chile.)
  
  Regiones de confinamiento y deconfinamiento a partir de propagadores no perturbativos en modelos 3-dimensionales
  Primeramente haremos una breve revisión acerca de las teorías de Yang-Mills y su cuantización a través de la integral de camino. Posteriormente, abordaremos el problema de Gribov, donde se estudia en profundidad la cuestión de la fijación del calibre de la teoría, generalizando la propuesta de Faddeev-Popov. A partir de este análisis es posible obtener modificaciones en la estructura analítica de los propagadores del gluón y del ghost en la región de infrarroja de la teoría, dando lugar a un escenario adecuado para el estudio del confinamiento del gluón. Tomando este escenario para el estudio no-perturbativo de las teorías de Yang-Mills, estudiaremos dos modelos en 3 dimensiones de gran interés físico, a saber, el conocido modelo de Georgi-Glashow (que introduce un campo de Higgs en la representación adjunta) y la llamada teoría de gauge topologicamente masiva, que introduce un término de Chern-Simons en la acción. En ambos casos, a través del análisis de los propagadores no-perturbativos del campo de calibre es posible determinar en el espacio de los parámetros de la teoría, regiones de existencia de polos físicos masivos para el gluón, correspondiendo a la fase masiva observable y regiones donde no es posible identificar gluónes como estados físicos pertenecientes a la matriz S, dando lugar a la fase confinante.
  (Arturo's presentation)
  
• Servio Pérez Merchancano (Departamento de Física, Grupo SENUMA, Universidad del Cauca, Popayán, Colombia)
  
  Quantum physics and transport process in 2D nanostructures by means of special functions
  In this paper we analyze quantum transport in a two-dimensional nanostructure where we consider the spin polarization, a physical effect which now has a high performance potential in research and fabricating of basic nano-spintronics devices for implementation and quantum computing operation [1]. We present a physical-mathematical analysis of effects of Dresselhaus \(H_D = \beta_D(\widehat\sigma_x k_x - \sigma_y k_y)\frac{\partial^2}{\partial z^2}\) and in-plane Rashba \(H_R = \alpha_R(\widehat\sigma_x k_y - \sigma_y k_x)\frac{\partial^2}{\partial z^2}\) spin-orbit interactions, where \(\beta_D\) and \(\alpha_R\) are constants depending on the material, \(\widehat\sigma_x\) and \(\widehat\sigma_y\) are Pauli matrices, \(k_x\) and \(k_y\) indicate the wave vectors in the crystallographic direction [100] and [101]. The effects spin-orbit coupling Schrödinger-Pauli equation given by the Hamiltonian end effects spin-orbit coupling Schrödinger-Pauli equation given by the Hamiltonian \begin{equation*} \widehat H = \frac{\hbar^2}{2m_j^*}(k_z^2 + k_{\parallel}^2)\widehat\sigma_x^T + V_{L,R}(z)\widehat\sigma_x^T + \widehat H_D + \widehat H_R + \widehat H_Z \end{equation*} [3,4,5] with a type potential energy barrier, shaped with a hyperbolic function, known as Pöschl-Teller, \(V_{L,R}(z) = V_0 \cosh^{-2} \frac{z-z_0}{a_{L,R}}\) where \(a_{L,R}\) refers to the width of the barriers [8] Furthermore considering the Zeeman energy \(\widehat H_z = \frac{1}{2} g_j^* \mu_B^j \widehat\sigma \cdot \vec B\) with the influence of in-plane magnetic field on spin polarization [7,9] The study is conducted analytically by confluent hypergeometric functions [6,2] allowing the resonant tunneling spin model for semiconductor heterostructures multilayer type. The results show spin polarization depending on the energy applied to the electrons, the well width and intensity of the magnetic field.

  Keywords: Polarisation, Dresselhaus, Rashba, Pöschl-Teller.

  References
  [1] P. S. Alekseev, M. M. Glazov, and S. A. Tarasenko. "Spin injection via (110)-grown semiconductor barriers". Phys. Rev. B 89 (15 Apr. 2014), p. 155306.
  [2] R. Beals and R. Wong. Special Functions: A Graduate Text. Cambridge University Press, 2010.
  [3] J.-D. Lu and J.-W. Li. "The effects of Dresselhaus and Rashba spin-orbit interactions on the electron tunneling in a non-magnetic heterostructure". Applied Surface Science 256.12 (2010), pp. 4027-4030.
  [4] J.-D. Lu and Y.-B. Li. "Effect of in-plane magnetic field on spin polarization in the presence of the Dresselhaus spin-orbit effect". Superlattices and Microstructures 48.6 (2010), pp. 517-522.
  [5] J.-D. Lu, X.-P. Xia, L. Yi, and Y.-H. Wang. "Spin-dependent resonant tunneling in a periodic non-magnetic heterostructure with spin-orbit effects". Physics Letters A 374.33 (2010), pp. 3341-3345.
  [6] A.F. Nikiforov and V.B. Uvarov. Special Functions of Mathematical Physics: A Unified Introduction with Applications. Springer Verlag, 2013.
  [7] M. Reza and K. Mahani. "Influence of in-plane magnetic field on spin polarization in the presence of the oft-neglected k3-Dresselhaus spin-orbit coupling". Physics Letters A 372.38 (2008), pp. 6022-6025.
  [8] A. Rodríguez and J. M. Cerveró. "One-dimensional disordered wires with Pöschl-Teller potentials". Phys. Rev. B 74 (10 Sept. 2006), p. 104201.
  [9] Q. Yan, J. Chen, H. Pan, and H. Xu. "Resonant tunneling in double-barrier structures under transverse magnetic field". Physica B: Condensed Matter 406.23 (2011), pp. 4361-4365.
• Andrés Reyes (Universidad de los Andes, Bogotá, Colombia)
  
  The Geometry of Quantum Phase Transitions: From Berry Phases to Fredholm Modules
  In the last few years, a characterization of the critical point in several spin chain modules in terms of Berry phases and also in terms of the so-called quantum geometric tensor has been extensively studied. This characterization complements the conformal field theory description of the critical point, as well as those based on entanglement properties of the ground state. In this talk I will present an approach based on the study of certain topological invariants that arise naturally from the topology of the parameter space of a modified XY-mode. This, in turn, leads to more general considerations in the context of quasi-free representations of CAR-algebras, for which a connection to noncommutative geometry via Fredholm modules can be exploited in the context of fermionic Gaussian systems.
• Inti Sodemann (Department of Physics, Massachusetts Institute of Technology, Cambridge, Massachusetts, USA)
  
  Applications of conformal field theory to the fractional quantum Hall states
  The fractional quantum Hall states are one of the most amazing quantum phases of matter. Among other mind bending features, they display quasiparticles with fractional charge and non-abelian braiding statistics. In this talk, I will revisit the use of conformal field theory machinery in the characterization of the ground state order and the edge and bulk quasiparticle excitations with particular emphasis on paired FQHE states.
  (Inti's presentation)
  

Poster session

• Julián Felipe Arcila Forero (Universidad Nacional de Colombia, Bogotá, Colombia) jfarcilaf@unal.edu.co)
  
  Phase transition of anyons confined in one-dimensional optical lattice
  (Julián's poster)
  
  Anyons are the third fundamental category of particles, for two anyons under particle exchange the wavefunction acquires a fractional phase \(e^{ i\theta}\), giving rise to fractional statistics with \( 0 < \theta < \pi\). The greatest interest for the anyons study emerged when the fractional quantum Hall effect observed experimentally had natural explanation in term of anyons.
  We study a Hubbard model for anyons equivalent to a variant of the Bose-Hubbard, we established an exact mapping between anyons and bosons in one-dimension. Using the density matrix renormalization group method we studied the system properties, we presented the phase diagram for density \(\rho=1\) with some angles, the quantum transition is from Mott insulator to Superfluid phase, the Mott lobe expands with increasing statistical angle.
  We study the block von Neumann entropy, which was used to establish the critical points. For a fixed density we study the critical point evolution vs \(\theta\) and find that the position of the critical point increasing with the angle. For fixing statistical we showed the dependency between the position of the critical point and the density, also the critical point decreases with increasing of the density, implying that the Mott region decreases.
  

  Joint with R. Franco y J. Silva-Valencia.

  Keywords: Anyons, phase transition, critical point, block von Neumann entropy.
• Óscar Casas (Universidad Nacional de Colombia, Bogotá, Colombia)
  
  Topological Insulators in Nanowires
  (Óscar's poster)
  
  In this work we review the main characteristics of a topological insulator and some applications in the study of nanowires. In particular, we summarize some results obtained for the energy spectrum in nanowires of circular and rectangular cross-section. In these systems the surface states show an energy gap associated with the Berry phase. Finally, we discuss how to control this gap using exchange fields and the possible applications in spintronics.
  

  Joint with S. Gomez P., Universidad el Bosque, Bogotá, Colombia and William J. Herrera, Universidad Nacional de Colombia, Bogotá, Colombia.
• Miguel Jorge Bernabe Ferreira (Universidade de São Paulo, Brasil)
  
  Further Explorations of the Parameter Space of \(3D\) Lattice Gauge Theories
  
  State sum models can be used to construct the partition functions of \(3D\) lattice gauge theories based on involutory Hopf algebras, \(\mathcal{A}\), of which the group algebras, \(\mathbb{C}G\), are a particular case. Transfer matrices can be obtained from such partition functions by carrying out the state sum construction on a manifold with boundary. The parameter space of these transfer contains various Hamiltonians of physical interest. The \(2D\) quantum double Hamitlonians of Kitaev can be obtained from such transfer matrices for specific values of these parameters. A initial study of such models has been carried out in our previous work. In this paper we study other regions of this parameter space to obtain some new and known models. The new model comprise of Hamiltonians which ``partially'' confine the excitations of the quantum double Hamiltonians which are usually deconfined. The state sum construction is not invariant by translations and thus it is natural to expect to obtain disordered Hamiltonians from the transfer matrices resulting from these constructions. Thus one set of known models consist of the disordered quantum double Hamiltonians. Finally we obtain quantum double Hamiltonians perturbed by magnetic or exchange fields which have been considered earlier in the literature to study the stability of topological order to perturbations.
• Mario Henao (Departamento de Física, Universidad Del Valle, Cali, Colombia,
  mario.henao@correounivalle.edu.co)
  
  Faraday rotation in thin metal films bounded by topological insulators
  (Mario's poster)
  
  Electromagnetic excitations arising in a metal slab surrounded by an insulator with a non trivial topology associated to time reversal symmetry (topological insulator) are described in the frame of axion electrodynamics. It is shown that the rotation of the polarization plane induced by the non trivial topology is a linear function of the topological term for all slab thicknesses but strongly depends on the dispersion relations of bonding and antibonding surface modes. Numerical calculations show that for the bonding surface modes the presence of the topological term leads to an increasing rotation angle, which becomes more pronounced for thin slabs. On the other hand, the rotation angle of polarization corresponding to antibonding surface modes decreases with the in-plane wave vector and its magnitude is several orders of magnitude greater than that corresponding to bonding modes.

  Joint with Juan Carlos Granada, Departamento de Física, Universidad Del Valle, Cali, Colombia

  References
  [1] J.C. Granada E and D.F. Rojas. "Local excitations in thin metal films bounded by topological insulators". Physica B: Condensed Matter 455 (Dec. 2014), pp. 82-84.
  [2] M. Z. Hasan, S.-Y. Xu, and M. Neupane. "Topological Insulators, Topological Crystalline Insulators, Topological Semimetals and Topological Kondo Insulators". (June 2014). arXiv:1406.1040.
  [3] A. Karch. "Surface plasmons and topological insulators". Physical Review B 83.24 (June 2011), p. 245432.
  [4] X.-L. Qi, T. L. Hughes, and S.-C. Zhang. "Topological field theory of time-reversal invariant insulators". Physical Review B 78.19 (Nov. 2008), p. 195424.
• Paul Marín (Grupo de Física Atómica y Molecular, Instituto de Física, Universidad de Antioquia, Medellín, Colombia)
  
  Simulation of universal logic quantum gates by using a toric code model
  (Paul's poster)
  
  Currently a topic of high scientific interest is the quantum simulation of many-body spin interactions. Toric code model is highlighted, in which the spins are located at the edges of a square lattice on the surface of a torus. In this paper the Hamiltonian of the system is initially identified. If the lattice is of dimension \(k\times k\), the Hamiltonian is a matrix of dimension \(2^{2k^2} \times 2^{2k^2}\). The many-qubit time evolution operator of the system is then obtained. Further to this, universal logic quantum gates are constructed. This work may have relevance to establish a representation of anyons by using the toric code model, which would simulate topological quantum gates.
  

  Joint with Jorge Mahecha, Universidad de Antioquia, Medellín, Colombia.

  Keywords: Many-electron systems, Quantum computation, anyons.

  References
  [1] E. Dennis, A. Kitaev, A. Landahl, and J. Preskill. "Topological quantum memory". J. Math. Phys. 43.9 (2002), p. 4452.
  [2] D. Gottesman. "Stabilizer Codes and Quantum Error Correction". Ph.D. Thesis, California Institute of Technology, Pasadena, 1997.
  [3] A.Yu. Kitaev. "Fault-tolerant quantum computation by anyons". Ann. Phys. 303.1 (2003), p. 2.
  [4] A.Yu. Kitaev. "Quantum computations: algorithms and error correction". Russ. Math. Surv. 52.6 (1997), p. 1191.
  [5] O. Viyuela, A. Rivas, and M.A. Martin-Delgado. "Generalized toric codes coupled to thermal baths". New J. Phys 14.3 (2012), p. 033044.
  [6] H. Weimer. "Quantum simulation of many-body spin interactions with ultracold polar molecules". Mol. Phys. 111.12 (2013), p. 1753.
• Óscar Martínez Castro (Facultad de Ciencias Básicas, Universidad del Atlántico, Barranquilla, Colombia)
  
  Density of states of a graphene layer under circularly polarized \(ac\) field
  
  In this work we study the density of states for a graphene monolayer in presence of circularly polarized ac field. In the effective mass approximation, the presence of photon-dressed electron states within an energy gap favors quantum oscillations in the density of states analogously to quantum magnetic oscillations in presence of quantizing magnetic field. Basically the difference lies in the nature of oscillations, which are driven by the field frequency.
  

  Joint with G. Salazar Cohen and R. Vega Monroy
• Carlos Mera Acosta (Instituto de Física, Universidade de São Paulo, Brazil, acosta@if.usp.br )
  
  Dirac Fermions without bulk backscattering in rhombohedral topological insulators
  
  The realization of a spintronic device using topological insulators is not trivial, because there are inherent difficulties in achieving the surface transport regime [1]. The majority of 3D topological insulators materials (3DTI) despite of support helical metallic surface states on an insulating bulk, forming topological Dirac fermions protected by the time-reversal symmetry [2,6], exhibit electronic scattering channels due to the presence of residual continuous bulk states near the Dirac-point [3]. From ab initio calculations, we studied the microscopic origin of the continuous bulk states in rhombohedral topological insulators materials with the space group \(D^{5}_{3d}(R\bar{3}m)\), showing that it is possible to understand the emergence of residual continuous bulk states near the Dirac-point into a six bands effective model, where the breaking of the \(R_{3}\) symmetry beyond the \(\Gamma\) point has an important role in the hybridization of the \(px\), \(py\) and \(pz\) atomic orbitals, which leads to a band repulsion that depends on only one parameter, as shown in the figure. Within this model, the mechanisms known to eliminate the bulk backscattering, for instance: the stacking faults [4], electric field [5] and alloy [7], generated a similar effect in the effective states of the 3DTI. Finally, we studied the surface electronic transport in the 3DTI with staking faults, showing how the surface electronic transport is modified by perturbations of bulk.

  
  
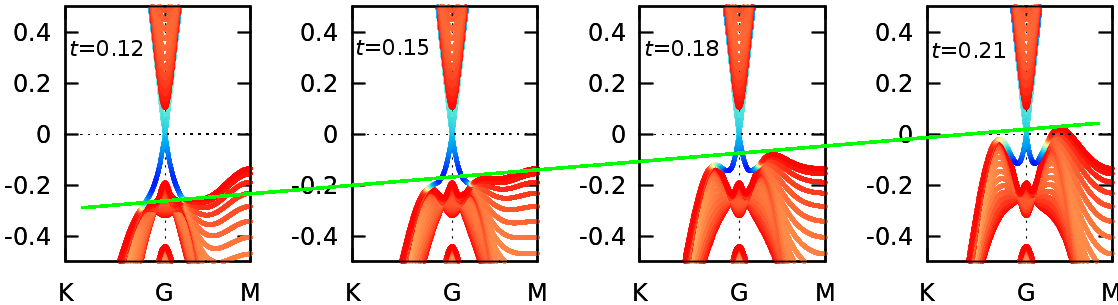
  Projected surface band structure for 20 Qls calculated using the six bands effective model varying the repulsion parameter. The color scale is related to the contribution of the Qls in the surface. The blue and red colors indicate the major and null contributions, respectively

  Joint with Antônio J. R. da Silva, Instituto de Física, Universidade de São Paulo y Laboratório Nacional de Luz Síncrotron, Campinas, Brasil y A. Fazzio, Laboratório Nacional de Luz Síncrotron, Campinas, Brasil

  References
  [1] L. Barreto et al. "Surface-Dominated Transport on a Bulk Topological Insulator". Nano Letters 14 (7 June 2014), pp. 3755-3760.
  [2] B. A. Bernevig. Topological insulators and topological superconductors. With Taylor L. Hughes. Princeton University Press, Princeton, NJ, 2013, pp. xii+247.
  [3] S. Kim et al. "Surface Scattering via Bulk Continuum States in the 3D Topological Insulator Bi2Se3 ". Phys. Rev. Lett. 107 (5 July 2011), p. 056803.
  [4] L. Seixas, L. B. Abdalla, T. M. Schmidt, A. Fazzio, and R. H. Miwa. "Topological states ruled by stacking faults in Bi2Se3 and Bi2Te3". Journal of Applied Physics 113.2, 023705 (2013), pages.
  [5] O. V. Yazyev, J. E. Moore, and S. G. Louie. "Spin Polarization and Transport of Surface States in the Topological Insulators Bi2 Se3 and Bi2 Te3 from First Principles". Phys. Rev. Lett. 105 (26 Dec. 2010), p. 266806.
  [6] H. Zhang, C.-X. Liu, X.-L. Qi, X. Dai, Z. Fang, and S.-C. Zhang. "Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface". Nature Physics 5 (May 2009), p. 438.
  [7] J. Zhang et al. "Band structure engineering in (Bi1-xSbx)2Te3 ternary topological insulators". Nature Communications 2.574 (2011).
• Nicolás Morales Durán, Andrés Vargas (Departamento de Matemáticas y Física, Universidad de los Andes, Bogotá, Colombia)
  
  A Bohmian approach to the non-Markovian non-linear Schrödinger-Langevin equation
  (Nicolás' and Andrés' poster)
  
  The theory of open quantum systems is of fundamental importance to properly describe real systems, which do not exist in complete isolation. Among the main approaches usually considered to incorporate environmental effects in the dynamics of the system under study, non-linear Schrödinger equations and system-plus-bath techniques are two of the most representative ones. In this work, a non-Markovian generalized Schrödinger-Langevin equation is derived from the system-plus-bath approach [1]. Specifically Bohmian mechanics is shown to be of great importance in order to obtain a compact expression for the damping potential, which reduces to the well known situations reported in the literature, where Markovian and/or non-linear effects are considered. Finally, an application regarding the generalized uncertainty principle (GUP) as a quantum gravitational principle is presented [2].
  

  Joint with Pedro Bargueño, Universidad de los Andes, Colombia, Bogotá.

  References
  [1] P. Bargueño. "Generalized uncertainty principle and quantum gravitational friction". Physics Letters B 727.4-5 (2013), pp. 496-499.
  [2] A. F. Vargas, N. Morales-Durán, and P. Bargueño. "A Bohmian approach to the non-Markovian non-linear Schrödinger-Langevin equation". Annals of Physics 356 (2015), pp. 498-504.
• Manuel Muñoz (Departamento de Física, Universidad Del Valle, Cali, Colombia, manuel.munoz@correounivalle.edu.co)
  
  Edge modes in the single-band Bose-Hubbard model
  
  Topological phases of matter are nowadays an active field of study and there is special interest in to look for their realization since there exists the possibility of topological superconductivity followed by the promise of a fault free quantum computer. On the other hand, ultra cold atoms have proven to be excellent quantum simulators to mimic the previously mentioned complex condensed matter systems. Therefore, in the present work, we use an already tested simulation of an Ising spin chain by taking advantage of the dipole transitions of the Mott-insulator state when the spins are in presence of a strong electric field. Furthermore, by means of a Jordan-Wigner transformation, the system is fermionized, and finally the unitary transformations introduced by Kitaev are used. The main result is that for a proper set of parameters the initial single-band Bose-Hubbard Hamiltonian can sustain unpaired zero-energy edge-modes.

  Joint with Karen Rodriguez and Javier Madroñero, Departamento de Física, Universidad Del Valle, Cali, Colombia

  References
  [1] I. Bloch, J. Dalibard, and S. Nascimbène. "Quantum simulations with ultracold quantum gases". Nature Physics 8.4 (Apr. 2012), pp. 267-276.
  [2] A. Y. Kitaev. "Unpaired Majorana fermions in quantum wires." Physics-Uspekhi 44.131 (2001).
  [3] X. Li, E. Zhao, and W. Vincent Liu. "Topological states in a ladder-like optical lattice containing ultracold atoms in higher orbital bands." Nature communications 4 (Jan. 2013), p. 1523.
  [4] S. Sachdev, K. Sengupta, and S. Girvin. "Mott insulators in strong electric fields". Physical Review B 66.7 (Aug. 2002), p. 075128.
  [5] J. Simon, W. S. Bakr, R. Ma, M. E. Tai, P. M. Preiss, and M. Greiner. "Quantum simulation of antiferromagnetic spin chains in an optical lattice." Nature 472.7343 (Apr. 2011), pp. 307-12.
  [6] S.-L. Zhu, Z.-D. Wang, Y.-H. Chan, and L.-M. Duan. "Topological Bose-Mott Insulators in a One-Dimensional Optical Superlattice". Physical Review Letters 110.7 (Feb. 2013), p. 075303.
• Mariela Nieto (Departamento de Física, Facultad de Ciencias Exactas, Universidad Nacional de La Plata, La Plata, Argentina, marielanieto@gmail.com)
  
  Effective Model for Graphene
  (Mariela's poster)
  
  We employ a simple nonrelativistic model, based on a deformation of the Heisenberg algebra which makes the commutator of momenta proportional to the pseudo-spin, to describe the low energy excitation of graphene. This model (which reduces in a ceratin limit to the usual linear one employed to describe these excitations as massless Dirac fermions) reproduces the leading (isotropic) terms in the low energy expansion of the dispersion relation derived from the tight binding model for both nearest and next-to-nearest-neighbor interactions. We solve the Landau problem for the resulting Hamiltonian and, taking into account the contribution of both Dirac points, we evaluated the Hall conductivity within a \(\zeta\)-function approach, showing that it is consisten with the \emph{anomalous integer quantum Hall effect} characteristic of graphene.
  

  Joint with H. Falomir, IFLP - CONICET and Departamento de Física, Facultad de Ciencias Exactas, Universidad Nacional de La Plata, La Plata, Argentina, J. Gamboa, Facultad de Física, Pontificia Universidad Católica de Chile, and Departamento de Física, Universidad de Santiago de Chile, Santiago, Chile, M. Loewe, Departamento de Física, Universidad de Santiago de Chile, Santiago, Chile and Centre for Theoretical and Mathematical Physics, University of Cape Town, South Africa.

  Keywords: Graphene, Hall conductivity, \(\zeta\)-function.
• José Luis Ribero (Universidad de Antioquia, Medellín, Colombia)
  
  Ramsey interferometer and measurements of quantum topological phases
  
  Ramsey's method of successive oscillatory fields is an accuracy procedure to perform molecular and atom beam resonance experiments. There exist a lot of advantages provided by this method. Between them, measurement of relative phases is the commonly used, this because the required information is available in the transition probability of the interferometer.
  Here we describe the Aharonov-Casher effect. Also we do a description of the Ramsey's interferometer and how it is used to measure topological phases.
  After that, we will describe how this interferometer is used to measure the phase acquired by the Aharonov-Casher effect in an atomic beam experiment
• Karen Valencia (Universidad del Atlántico, Baranquilla, Colombia)
  
  Medidas de impedancia del \(Dy_2Fe_{17-x}Ga_x\) cerca de la transición de fase Ferromagnética-Paramagnética
  (Karen's poster)
  
  Estudio de las propiedades de transporte eléctrico de los compuestos intermetálicos con composición \(Dy_2 Fe_{17-x}Ga_x\) (\(x = 0, 1, 3, 4, 5, 7\)) en el rango cercano a la temperatura de transición (Tc) de cada uno de estos compuestos. Para ello, se llevó a cabo medidas de impedancia como función de la temperatura, en un rango de frecuencia comprendido entre 1 Hz a 1 MHz utilizando la técnica de espectroscopia de impedancia. Además se realizaron medidas de difracción de rayos X (DRX) a temperatura ambiente, como método de caracterización estructural, el cual permitió conocer los parámetros de red del compuesto y confirmar la formación de una sola fase principal. Las estructuras cristalinas se refinaron a partir de sus patrones de difracción empleando el método de Rietveld, revelando que la sustitución de Ga en la serie ocasiona un aumento en los parámetros de red y un cambio en su estructura de la fase hexagonal tipo \(Th_2Ni_{17}\) a la fase romboédrica tipo \(Th_2Zn_{17}\).

• Greis Julieth Cruz Reyes (Universidad Nacional de Colombia, Bogotá)
  
  (Greis's poster)
  
• Stefany Murcia (Universidad Nacional de Colombia, Bogotá)
  
  (Stefany's poster)