 |
Johannes RauDepartament of MathematicsFaculty of Science  |
Start
I work at the Departament of Mathematics at the Universidad de los Andes, Bogotá, Colombia. My research area is tropical geometry and its connections to enumerative geometry, real algebraic geometry and intersection theory. More general, my mathematical interests focus on algebraic geometry, symplectic geometry and combinatorics. For more details, please check out the other sections and contact me.
Email: j.rau (at) uniandes.edu.co
News
MCA Session "Tropical Geometry, twistor spaces and cluster geometry"
I am currently organizing the Special Session "Tropical Geometry, twistor spaces and cluster geometry" at the Mathematical Congress of the Americas 2025 in Miami. My coorganizers are Helge Ruddat, Lara Bossinger and Lucia Lopez de Medrano. Here are some links for more information.

- Website MCA 2025
- List of Special Sessions (ours is 35)
Colombian Encounter of Tropical and Non-archimedean Geometry
Together with Pablo Cubides, I organized the school and workshop "Colombian Encounter of Tropical and Non-archimedean Geometry". Here is the link to the event website.

LAGARTOS
We organized the biweekly Latino-Americano Geometría Algebráica Real y Tropical Online Seminario (LAGARTOS). Lagartos is Spanish for lizards.
Patchworking Online
Conhstruct your personal real algebraic curve with this browser app.
Book
I write a book on tropical geometry together with Grigory Mikhalkin. You can find a draft version here. Comments and corrections are highly welcome.
Research
Keywords
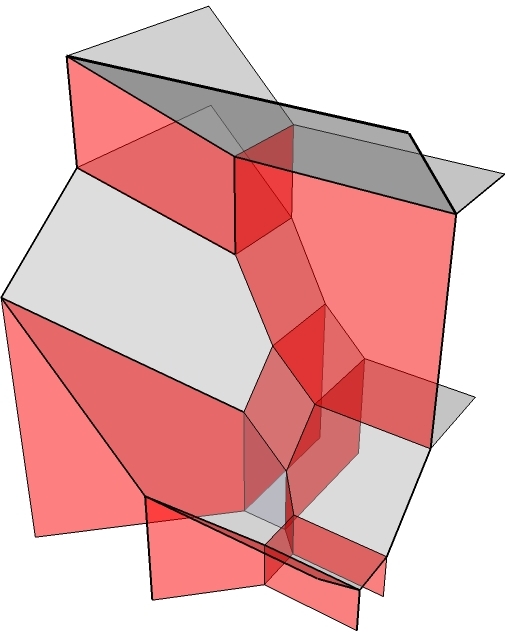
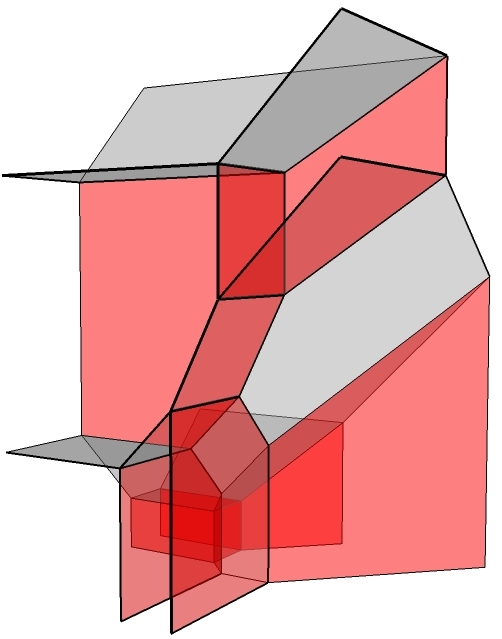
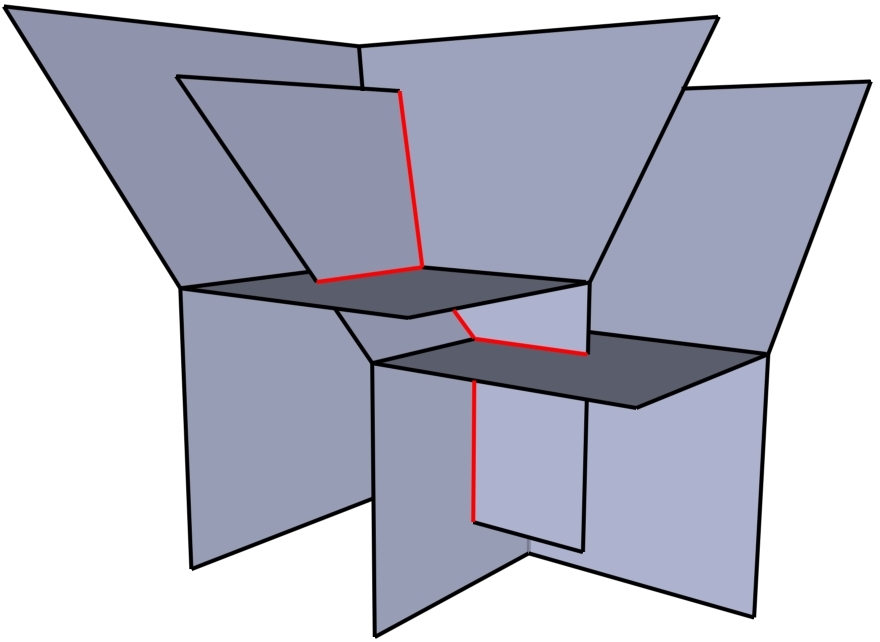
 My research area is tropical
geometry (the fancy adjective tropical was originally used in
the context of the max-plus algebra to honour earlier work of the
Brazilian (Hungarian-born) mathematician Imre
Simon). Even though the origins of the field are much older,
tropical geometry emerged as an new trend in algebraic and
symplectic geometry around 2000. Here is a list of keywords
describing my research interests.
My research area is tropical
geometry (the fancy adjective tropical was originally used in
the context of the max-plus algebra to honour earlier work of the
Brazilian (Hungarian-born) mathematician Imre
Simon). Even though the origins of the field are much older,
tropical geometry emerged as an new trend in algebraic and
symplectic geometry around 2000. Here is a list of keywords
describing my research interests.
- (Real) enumerative geometry
- Real Hurwitz numbers
- Descendant Gromov-Witten invariants, Psi classes
- Topology of real algebraic varieties
- Hilbert's 16th problem for nodal curves
- Real algebraic surfaces
- Intersection theory and Hodge theory
- Tropical intersection products
- Matroids
- Tropical Hodge groups
- Rational equivalence
-
Book
I write a book on tropical geometry together with Grigory Mikhalkin. You can find a draft version here. Comments and corrections are highly welcome.
Tropical geometry (draft)
Dinosaurs and skeletons
Tropical geometry for non-mathematicians
Tropical mathematics can be compared to the world of dinosaurs.
When paleontologists
want to learn more about these animals, they can't just go watch them in the
zoo or the jungle, because unfortunately the poor things became
extinct a long time ago. Instead, they work more like
 archeologists. They go digging for their bones, try to reassemble
their skeletons, and from that draw conclusions about how these
animals looked like, what they ate, how they hunted etc. In tropical
geometry, we do exactly the same!
archeologists. They go digging for their bones, try to reassemble
their skeletons, and from that draw conclusions about how these
animals looked like, what they ate, how they hunted etc. In tropical
geometry, we do exactly the same!
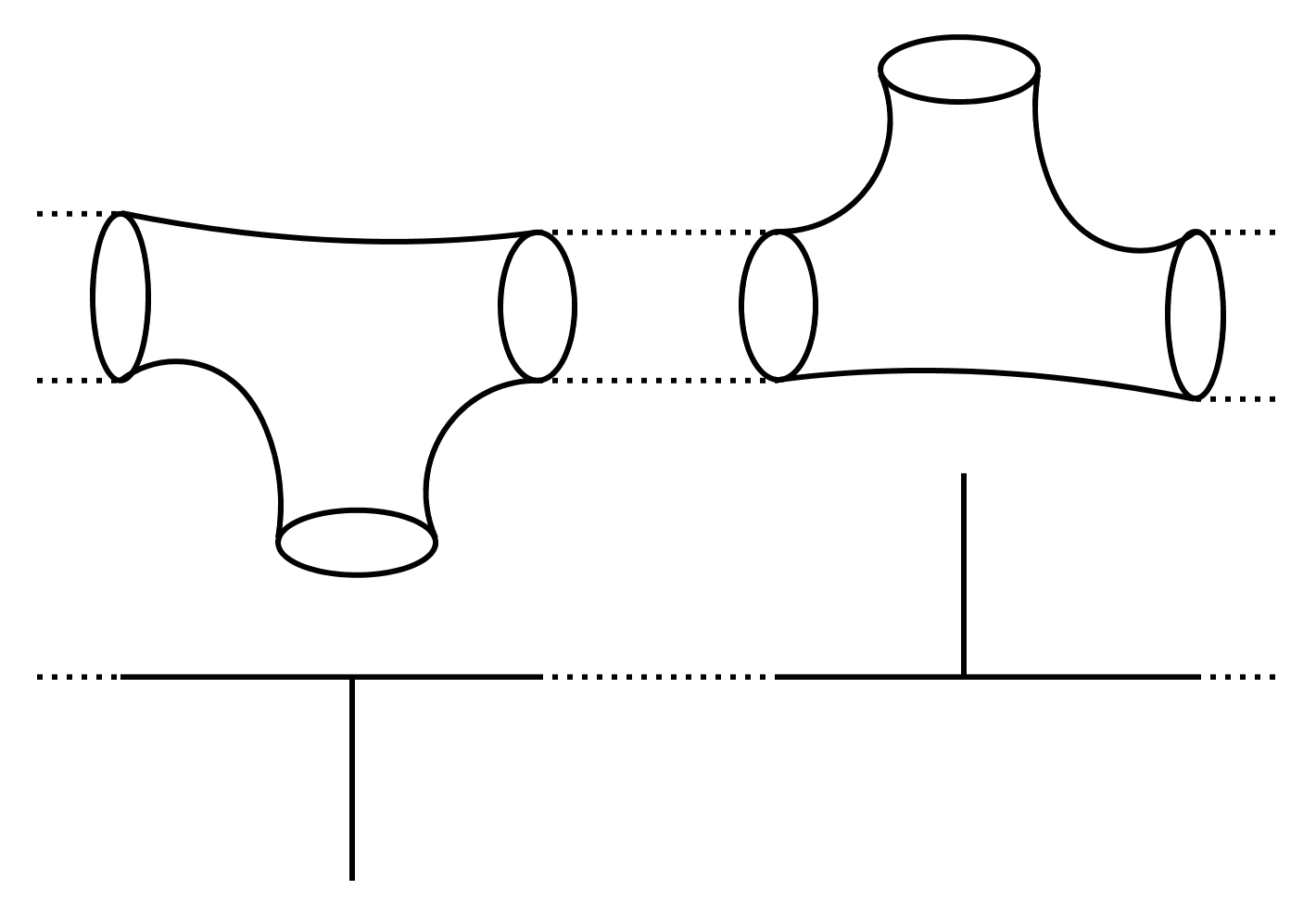
In our setting, the dinosaurs are called algebraic varieties. These are complicated geometrical shapes given by polynomial equations. Algebraic varieties show up all the time in mathematics, science and real life, and therefore their study forms one of the oldest and most sophisticated fields in mathematics (called algebraic geometry). Algebraic varieties are often so complicated that it is impossible to get our hands on them directly – like the extinct dinosaurs. However, in some cases mathematicians found a way to dig out the skeletons of these mathematical dinosaurs. Technically, you first have to turn the dinosaurs into amoebas and then starve them out until only their skeletons are left ;).
The mathematical skeletons are called tropical varieties, and in tropical geometry we play paleontologist and try to find out more about the original geometrical objects by studying their tropical skeletons (you can find some pictures on this page). The nice thing is that tropical varieties are much simpler objects than the original ones and can be studied in much more down-to-earh terms. Of course, we cannot work wonders and find answer to all questions (it is easy to estimate the size of the real-life dinosaur from its skeleton, but did it have furry or smooth skin?), but by now some remarkable facts about algebraic varieties were deduced from the study of their tropical skeletons, and that is why tropical geometry is at the moment such an exciting and steadily growing field.
Further Resources
Tropical geometry for students/mathematicians from other fields
You are bachelor/master student in mathematics (or a researcher from a different field) and want to embark on a first expedition to the tropics? Then have a look at these lecture notes.
These notes grew out of a lecture series I gave for bachelor students without any prior knowlwedge of the topic. They are therefore on a very elementary level and give priority to intution and illustrations as opposed to rigour and depth.
Presentations
A few slides with more info on some projects.
- The dimension of amoebas
- Hilbert in the Tropics – Topology of real (nodal) curves
- Tropical Enumerative Geometry
- Tropical counts of real Hurwitz numbers (partially in German)
Combinatorial Patchworking
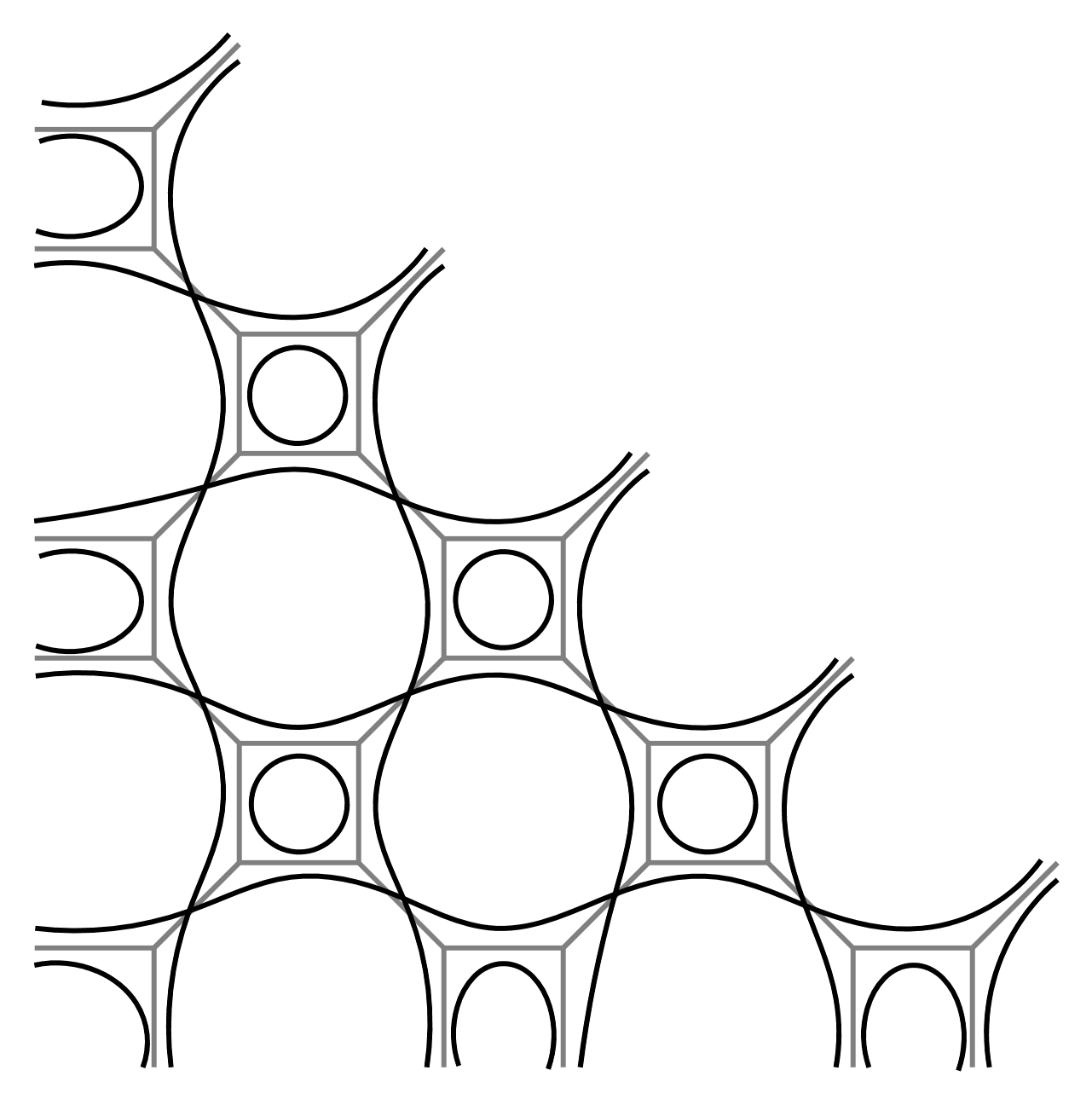
One of the origins of tropical geometry is Viro's patchworking method. The link below leads to a small browser app which allows you to do some experiments with this method.
You can use it to create your own real algebraic curves and pictures like the one to the right. It shows the (topological) shape of a planar real algebraic curve of degree 30 (that is, the set of zeros of a polynomial of degree 30 in the variables x and y). You can find some information on this topic in the following slides.
Publications
Artículos
Preprints
- [1]
-
Johannes Rau, Arthur Renaudineau, and Kris Shaw. Real phase structures on tropical manifolds and patchworks in higher codimension. Preprint (2023). arXiv: 2310.08313.
- [2]
-
Jan Draisma, Sarah Eggleston, Rudi Pendavingh, Johannes Rau, and Chi Ho Yuen. The amoeba dimension of a linear space (2023). arXiv: 2303.13143.
Published
- [3]
-
Erwan Brugallé, Lucía López de Medrano, and Johannes Rau. Combinatorial patchworking: back from tropical geometry. Trans. Amer. Math. Soc. (accepted) (2022). arXiv: 2209.14043.
- [4]
-
Johannes Rau. Real semi-stable degenerations, real-oriented blow-ups and straightening corners. Int. Math. Res. Notices 2023.18 (2023), pp. 15896–15927. doi: 10.1093/imrn/rnad005. arXiv: 2203.17097.
- [5]
-
Johannes Rau, Arthur Renaudineau, and Kris Shaw. Real phase structures on matroid fans and matroid orientations. J. Lond. Math. Soc. 106.4 (2022), pp. 3687–3710. doi: 10.1112/jlms.12671. arXiv: 2106.08728.
- [6]
-
Johannes Rau. On the tropical Lefschetz-Hopf trace formula. J. Algebraic Combin. (2023). doi: 10.1007/s10801-023-01220-y. arXiv: 2010.07901.
- [7]
-
Johannes Rau. The tropical Poincaré-Hopf theorem. J. Combin. Theory Ser. A 196 (2023), p. 105733. doi: 10 . 1016 / j . jcta . 2023 . 105733. arXiv: 2007.11642.
- [8]
-
Grigory Mikhalkin and Johannes Rau. Spines for amoebas of rational curves. Enseign. Math. 65 (2 2019), pp. 377–396. doi: 10.4171/LEM/65-3/4-3. arXiv: 1906.04500.
- [9]
-
Jan Draisma, Johannes Rau, and Chi Ho Yuen. The dimension of an amoeba. Bull. London Math. Soc. 52.1 (2020), pp. 16–23. doi: 10.1112/blms.12301. arXiv: 1812.08149.
- [10]
-
Johannes Rau. Lower bounds and asymptotics of real double Hurwitz numbers. Math. Ann. 375.1-2 (2019), pp. 895–915. doi: 10.1007/s00208-019- 01863-y. arXiv: 1805.08997.
- [11]
-
Boulos El Hilany and Johannes Rau. Signed counts of real simple rational functions. J. Algebraic Combin. 52.3 (2020), pp. 369–403. doi: 10.1007/s10801- 019-00906-6. arXiv: 1712.05639.
- [12]
-
Philipp Jell, Johannes Rau, and Kristin Shaw. Lefschetz (1,1)-theorem in tropical geometry. Épijournal Géom. Algébrique 2.11 (2018). doi: 10. 46298/epiga.2018.volume2.4126. arXiv: 1711.07900.
- [13]
-
Ilia Itenberg, Grigory Mikhalkin, and Johannes Rau. Rational quintics in the real plane. Trans. Amer. Math. Soc. 370 (2018), pp. 131–196. doi: 10.1090/ tran/6938. arXiv: 1509.05228.
- [14]
-
Hannah Markwig and Johannes Rau. Tropical Real Hurwitz numbers. Math. Z. 281.1-2 (2015), pp. 501–522. doi: 10.1007/s00209- 015- 1498- 4. arXiv: 1412.4235.
- [15]
-
Mathieu Guay-Paquet, Hannah Markwig, and Johannes Rau. The Combinatorics of Real Double Hurwitz Numbers with Real Positive Branch Points. Int. Math. Res. Not. 2016.1 (2016), pp. 258–293. doi: 10. 1093/imrn/rnv135. arXiv: 1409.8095.
- [16]
-
Lars Allermann, Simon Hampe, and Johannes Rau. On rational equivalence in tropical geometry. Canad. J. Math. 68.2 (2016), pp. 241–257. doi: 10. 4153/CJM-2015-036-0. arXiv: 1408.1537.
- [17]
-
Georges François and Johannes Rau. The diagonal of tropical matroid varieties and cycle intersections. Collect. Math. 64.2 (2013), pp. 185–210. doi: 10.1007/s13348-012-0072-1. arXiv: 1012.3260.
- [18]
-
Johannes Rau. Intersections on tropical moduli spaces. Rocky Mt. J. Math. 46.2 (2016), pp. 581–662. doi: 10.1216/RMJ-2016-46-2-581. arXiv: 0812.3678.
- [19]
-
Hannah Markwig and Johannes Rau. Tropical descendant Gromov-Witten invariants. Manuscr. Math. 129.3 (2009), pp. 293–335. doi: 10.1007/s00229- 009-0256-5. arXiv: 0809.1102.
- [20]
-
Lars Allermann and Johannes Rau. First steps in tropical intersection theory. Math. Z. 264.3 (2010), pp. 633–670. doi: 10.1007/s00209-009-0483-1. arXiv: 0709.3705.
Others
- [21]
-
Johannes Rau. A First Expedition to Tropical Geometry. Lecture notes for a mini course given at the International School on Topological and Geometric Combinatorics, Tehran, Iran, 13–16/02/2017. 2018. url: https://math.uniandes.edu.co/~j.rau/downloads/FirstExpedition.pdf.
- [22]
-
Grigory Mikhalkin and Johannes Rau. Tropical Geometry. textbook in preparation. 2019. url: https://math.uniandes.edu.co/~j.rau/downloads/main.pdf.
- [23]
-
Boulos El Hilany, Johannes Rau, and Arthur Renaudineau. Combinatorial patchworking tool. Javascript applet. 2017. url: https://math.uniandes.edu.co/~j.rau/patchworking/patchworking.html.
- [24]
-
Johannes Rau. Tropical intersection theory and gravitational descendants. PhD-Thesis. Technische Universität Kaiserslautern, 2009. url: http://kluedo.ub.uni-kl.de/volltexte/2009/2370/.
Presentations
- The dimension of amoebas
- Hilbert in the Tropics – Topology of real (nodal) curves
- Tropical Enumerative Geometry
- Tropical counts of real Hurwitz numbers (partially in German)
- Polyeder – eine (T)Raumreise (talk for high schools/wider audiences, in German)
Selected Talks
- 17/12/2019 MATRIX conference “Tropical geometry and mirror symmetry”, Creswick, Australia
- 01/10/2019 Workshop “Regensburg days on non-archimedean and tropical geometry”, Regensburg, Germany
- 13/09/2019 CMO Workshop “Tropical Methods in Real Algebraic Geometry”, Oaxaca, Mexico
- 29/04/2019 MFO-Workshop “Tropical Geometry: new directions”, Oberwolfach, Germany
- 22/01/2019 Seminar “Diskrete Mathematik/Geometrie”, TU Berlin, Germany
- 16/01/2019 Seminar “Topologie Algèbre et Géométrie”, Université de Nantes, France
- 03/12/2018 Colloquium talk, Universität Bern, Switzerland
- 02–04/05/2018 Lecture Series “Tropical methods in real algebraic geometry”, ASGARD math meeting, U Oslo, Norway
- 22/03/2018 Workshop on Moduli spaces of curves and mirror symmetry, IML Stockholm, Sweden
- 28/11/2017 Workshop “Young Researchers in String Mathematics”, MPI Bonn, Germany
- 13–16/02/2017 Lecture series “Tropical geometry”, School on Topological and Geometric Combinatorics, Tehran, Iran
- 11/01/2016 German-Israeli Workshop in Algebraic and Tropical Geometry, Tel Aviv, Israel
- 12/06/2015 AMS-EMS-SPM International Meeting, Session on Moduli Theory, Porto, Portugal
- 01/05/2015 MFO-Workshop “Tropical Aspects in Geometry, Topology and Physics”, Oberwolfach, Germany
- 18/09/2014 Meeting of the German and Polish mathematical societies, Real Algebraic Geometry workshop, Poznán, Poland
- 03/04/2013 Seminar “Géométrie tropicale”, Institut de Mathématiques de Jussieu, Paris, France
- 23/05/2011 Seminar “Géométrie symplectique”, Institut de Recherche Mathématique Avancée, Strasbourg, France
- 04/04/2008 Combinatorics seminar at the University of Michigan, Ann Arbor, USA
Organization of conferences
- 27–31/03/2017 Conference “Tropical curve counts, motivic integration and nonarchimedean geometry”, Universität Tübingen (joint with Hannah Markwig)
- 14–18/09/2015 Conference “Tropical Geometry in the Alps”, Les Diablerets, Switzerland (joint with Kristin Shaw, Grigory Mikhalkin)
- 24–28/11/2014 Closing conference of the TROPGEO project, Saas Fee, Switzerland (joint with Grigory Mikhalkin)
- 20/02/2013 Meeting of the seminar “Tropical Geometry in Europe”, Universität des Saarlandes (joint with Hannah Markwig)
- 17–20/09/2012 Minisymposium of the DMV annual meeting in Saarbrücken (joint with Hannah Markwig)
- 18–21/12/2011 Conference “Perspectives in Tropical Geometry 2011”, Arolla, Switzerland (joint with Grigory Mikhalkin)
Teaching
Courses
Students Seminars
Working group seminars
|
|
Contact
|
j.rau (at) uniandes.edu.co Postal address
Departamento de Matemáticas |
Phone
Phone: +57 1 3394949 Office
Room H-304 |


