 |
Johannes RauFachbereich MathematikFakultät der Naturwissenschaften  |
Start
Ich arbeite am Fachbereich Mathematik an der Universidad de los Andes, Bogotá, Kolumbien. Mein Forschungsgebiet ist die tropische Geometrie in Verbindung zu enumerativer Geometrie, reeller algebraischer Geometrie und Schnitttheorie. Allgemein liegt mein mathematischer Schwerpunkt in der algebraischen Geometrie, der symplektischen Geometrie und der Kombinatorik. Mehr Details gibt es in den folgenden Abschnitten oder per Email.
Email: j.rau (at) uniandes.edu.co
Aktuell
MCA Session "Tropical Geometry, twistor spaces and cluster geometry"
Aktuell organisiere ich die Special Session "Tropical Geometry, twistor spaces and cluster geometry" für den Mathematical Congress of the Americas 2025 in Miami. Meine Mitorganisatoren sind Helge Ruddat, Lara Bossinger and Lucia Lopez de Medrano. Unter den folgenden Links gibt es weitere Informationen.

- Webseite MCA 2025
- Liste der Special Sessions (unsere ist 35)
Colombian Encounter of Tropical and Non-archimedean Geometry
Zusammen mit Pablo Cubides habe ich die Schule und Konferenz "Colombian Encounter of Tropical and Non-archimedean Geometry" organisiert. Hier ist der Link zur Webseite des Events.

LAGARTOS
Wir organisierten das Latino-Americano Geometría Algebráica Real y Tropical Online Seminario (LAGARTOS). Lagartos sind übrigens Eidechsen.
Patchworking Online
Konstruiere deine eigene reelle algebraische Kurve mit dieser einfachen Browseranwendung.
Buch
Ich schreibe ein Buch über tropische Geometrie zusammen mit Grigory Mikhalkin. Der folgende Link führt zur aktuellen Entwurfsfassung. über Anregungen und Verbesserungen aller Art freue ich mich sehr.
Forschung
Schlagwörter
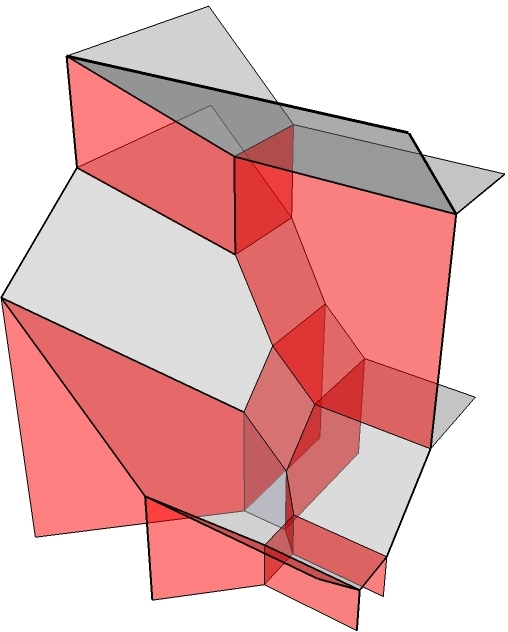
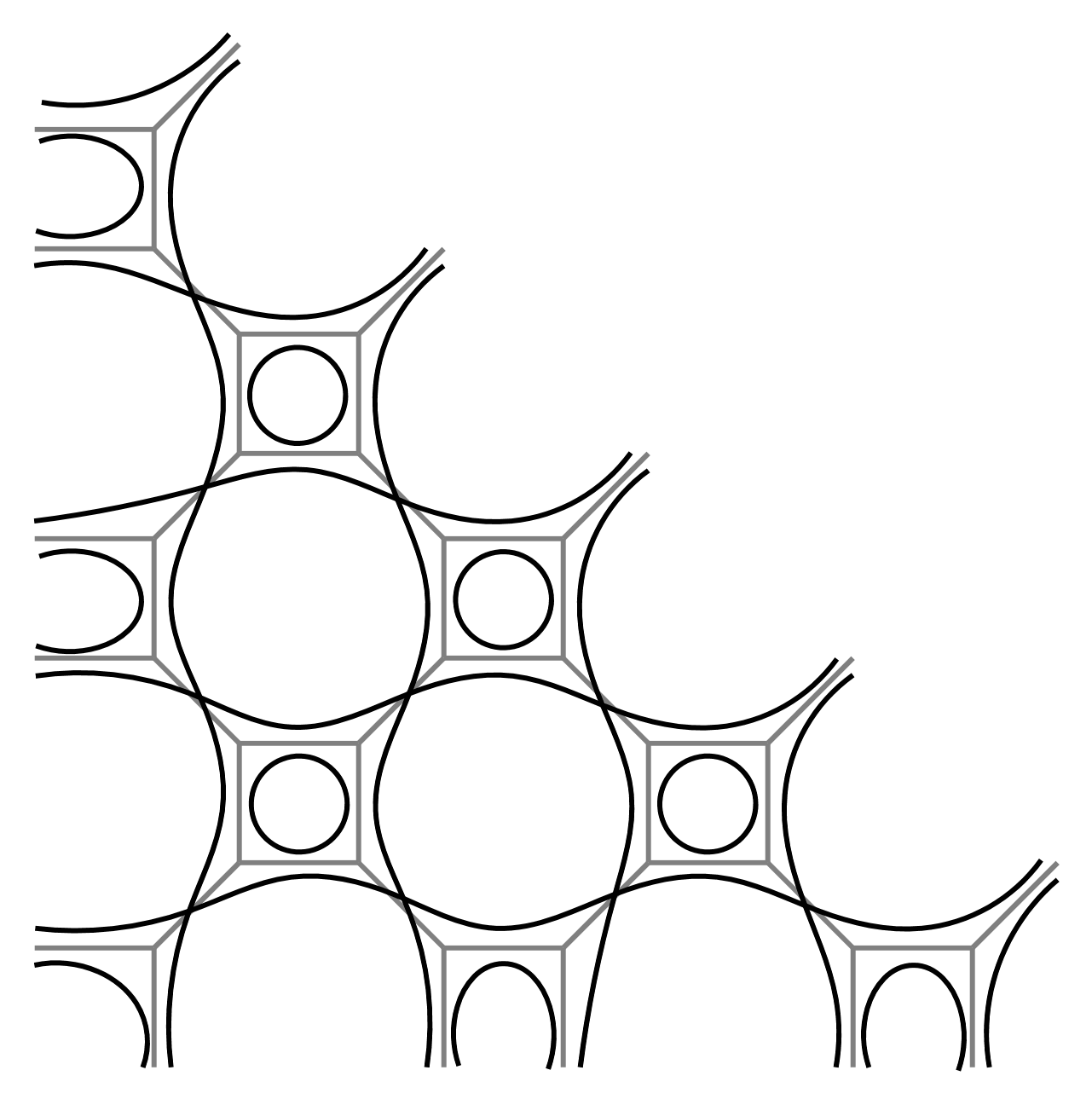 Mein Forschungsgebiet ist die tropische
Geometrie (der Ursprung des exotischen Namens ist recht
langweilig – ursprünglich wurde das Adjektiv "tropisch" im
Zusammenhang mit der Max-Plus-Algebra zu Ehren des brasilianischen
(in Ungarn geborenen) Mathematikers Imre
Simon verwendet). Auch wenn die Ursprünge des Gebietes weiter
zurück liegen, entstand tropische Geometrie als neue Entwicklung in
der algebraischen und symplektischen Geometrie um das Jahr 2000.
Meine spezifischen Interessen möchte ich anhand einer kurzen Liste
von Stichworten darstellen.
Mein Forschungsgebiet ist die tropische
Geometrie (der Ursprung des exotischen Namens ist recht
langweilig – ursprünglich wurde das Adjektiv "tropisch" im
Zusammenhang mit der Max-Plus-Algebra zu Ehren des brasilianischen
(in Ungarn geborenen) Mathematikers Imre
Simon verwendet). Auch wenn die Ursprünge des Gebietes weiter
zurück liegen, entstand tropische Geometrie als neue Entwicklung in
der algebraischen und symplektischen Geometrie um das Jahr 2000.
Meine spezifischen Interessen möchte ich anhand einer kurzen Liste
von Stichworten darstellen.
- (Reelle) enumerative Geometrie
- Reelle Hurwitz-Zahlen
- Abgeleitete Gromov-Witten-Invarianten, Psi-Klassen
- Topologie von reellen algebraischen Varietäten
- Hilberts 16. Problem für nodale Kurven
- Reelle algebraische Flächen
- Schnitttheorie und Hodge-Theorie
- Tropische Schnittprodukte
- Matroide
- Tropische Hodge-Gruppen
- Rationale äquivalenz
-
Buch
Ich schreibe ein Buch über tropische Geometrie zusammen mit Grigory Mikhalkin. Der folgende Link führt zur aktuellen Entwurfsfassung. über Anregungen und Verbesserungen aller Art freue ich mich sehr.
Tropical geometry (Entwurf)
Dinosaurier und Skelette
Tropische Geometrie für Nicht-Mathematiker
Wir wagen uns hier an einen Vergleich der tropischen Mathematik mit der Welt der
Dinosaurier. Wenn Paläontologen
mehr über diese Tiere erfahren möchten, können sie nicht einfach in
den Zoo oder den Urwald spazieren, denn unglücklicherweise sind die
armen Viecher schon vor langer Zeit ausgestorben. Stattdessen
arbeiten sie eher wie Archäologen. Sie graben nach den versteinerten
Knochen, versuchen die Skelette zu
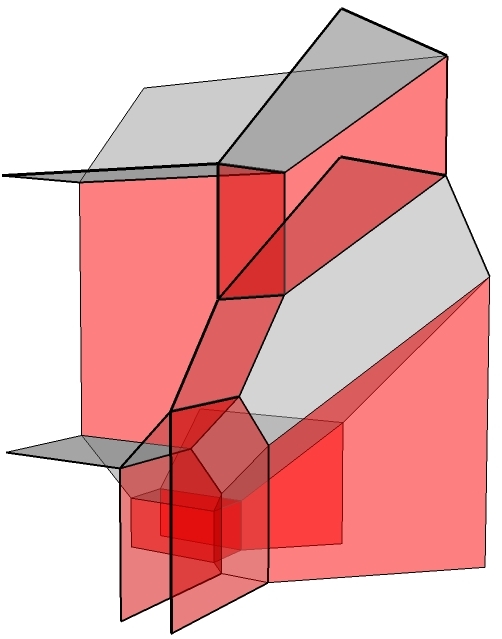 rekonstruieren und ziehen dann Rückschlüsse darüber, wie diese Tiere
aussahen, was sie aßen, wie sie jagten usw. In der tropischen
Geometrie machen wir genau das Gleiche!
rekonstruieren und ziehen dann Rückschlüsse darüber, wie diese Tiere
aussahen, was sie aßen, wie sie jagten usw. In der tropischen
Geometrie machen wir genau das Gleiche!
In unserer Welt werden die Dinosaurier "algebraische Varietäten" genannt. Dabei handelt es sich um komplizierte geometrische Formen beschrieben durch polynomiale Gleichungen. Solche algebraische Varietäten tauchen in der Mathematik, den Naturwissenschaften aber auch im echten Leben ständig auf, und daher bildet ihr Studium eines der ältesten und mächtigsten Gebiete der Mathematik (die sogenannte algebraische Geometrie). Algebraische Varietäten sind oft so komplizert, dass es unmöglich ist, sie direkt in den Griff zu kriegen – genau wie bei den ausgestorbenen Dinosauriern. In manchen Fällen haben es Mathematiker allerdings geschafft, die Skelette dieser mathematischen Dinosaurier auszugraben. Konkret muss man die Dinosaurier zunächst in Amöben verwandeln und sie dann so lange verhungern lassen bis nur noch ihre Skelette übrig sind ;).
Diese mathematischen Skelette nennen sich tropische Varietäten (auf diesr Seite finden sich einige Abbildungen davon). In der tropischen Geometrie spielen wir also Paläontologe und versuchen, mehr über die ursprünglichen geometrischen Objekte anhand ihrer tropischen Skelette zu erfahren. Der Vorteil ist, dass tropische Varietäten viel einfacher sind als die ursprünglichen Objekte und daher mit viel elementareren Methoden untersucht werden können. Natürlich vollbringt der tropische Ansatz keine Wunder (es ist einfach, die Größe eines Dinosauriers anhand seines Skelettes abzuschätzen, aber hat er nun eine glatte oder behaarte Haut?), aber mittlerweile gibt es eine Reihe von bemerkenswerten Fakten über algebraische Varietäten, die aus dem Studium ihrer tropischen Skelette geschlussfolgert wurden. Und deshalb ist tropische Geometrie zur Zeit ein spannendes und immer weiter wachsendes Arbeitsgebiet.
Weitere Materialien
Tropische Geometrie für Studenten/Mathematiker aus anderen Bereichen
Du bist Bachelor/Master Student für Mathematik oder Forscher in einem anderen Bereich und möchtest dich auf eine erste Expedition in die Tropen wagen? Dann ist dieses kurze Skript vielleicht das Richtige.
Dieses Skript entstand aus einem Kompaktkurs für Bachelor Studenten ohne Vorkenntnisse zum Thema. Das Level ist darum sehr elementar, und der Schwerpunkt liegt auf Intuition und Veranschaulichung gegenüber Exaktheit und Tiefe.
Vorträge
Einige Folien mit weiteren Infos zu ein paar Projekten.
- The dimension of amoebas
- Hilbert in the Tropics – Topology of real (nodal) curves
- Tropical Enumerative Geometry
- Tropical counts of real Hurwitz numbers (teilweise auf Deutsch)
Kombinatorisches Patchworking
Einer der Vorläufer der tropischen Geometrie ist Viro's Patchworking Methode. Diese Methode erlaubt es, reelle algebraische Varietäten mit bestimmten topologischen Eigenschaften zu konstruieren. Unter dem folgenden Link findest du eine kleine Browseranwendung, mit der du die Methode selbst ausprobieren kannst.
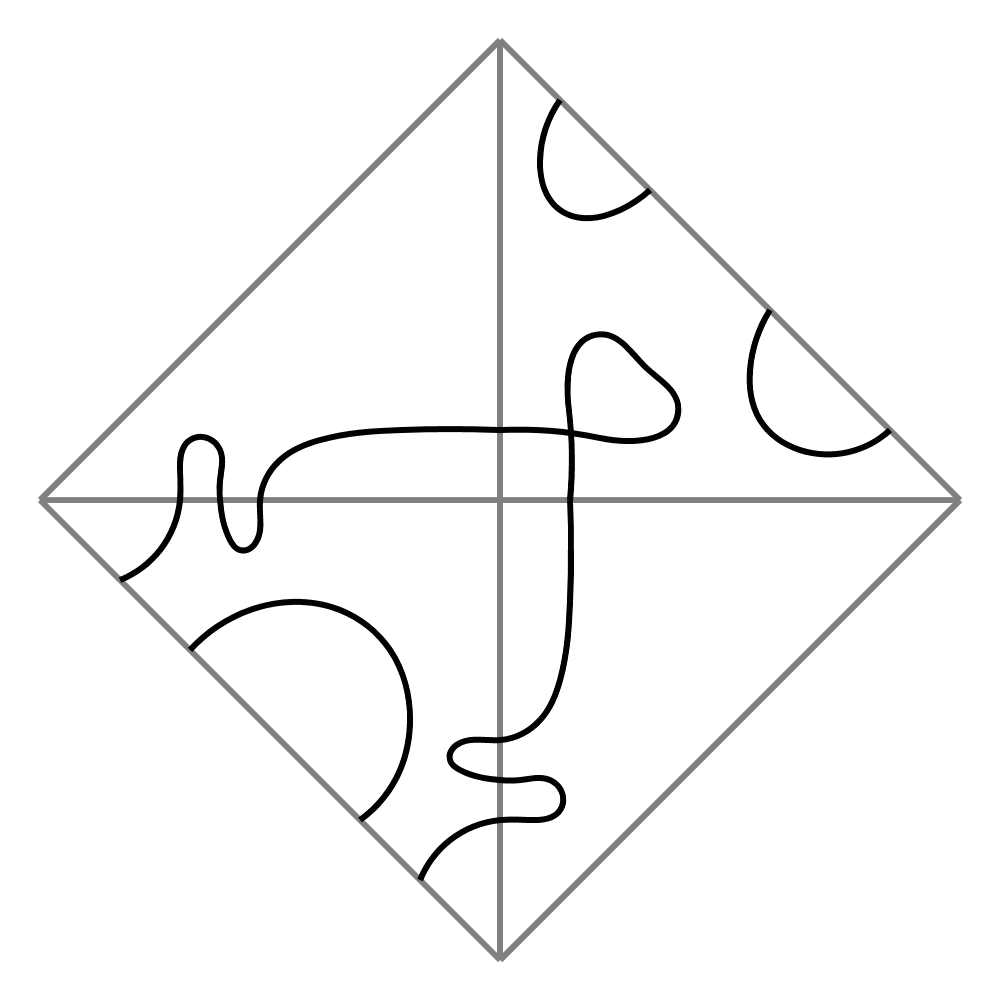
Damit kannst du deine eigene reelle algebraische Kurve und hübsche Bilder wie das nebenstehende erzeugen. Es zeigt schematisch die (topologische) Form einer ebenen reellen algebraischen Kurve vom Grad 30 (das heißt, die Nullstellen eines Polynoms vom Grad 30 in den Variablen x und y). In den folgenden Folien findest du einige weitere Informationen zu diesem Thema.
Publikationen
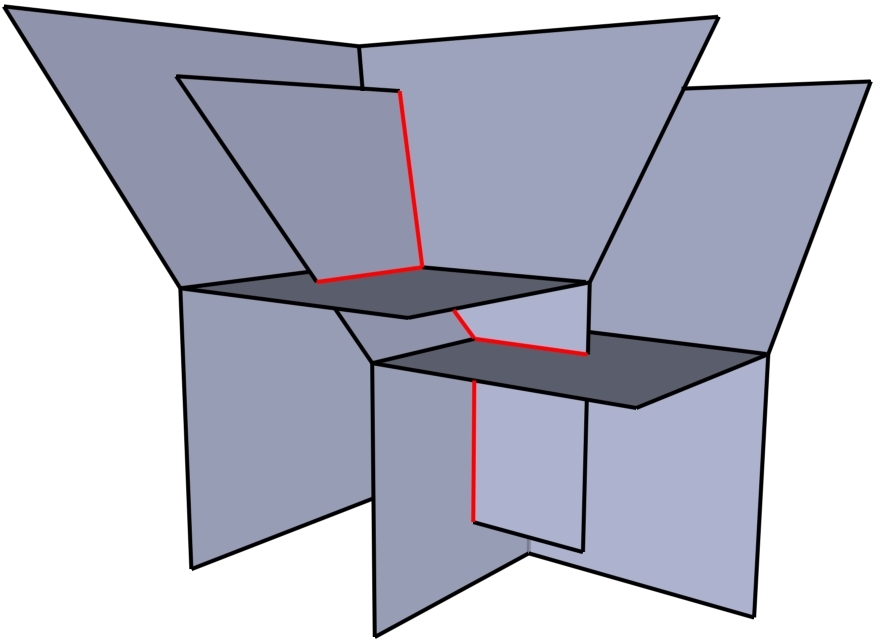
Artikel
Preprints
- [1]
-
Johannes Rau, Arthur Renaudineau, and Kris Shaw. Real phase structures on tropical manifolds and patchworks in higher codimension. Preprint (2023). arXiv: 2310.08313.
- [2]
-
Jan Draisma, Sarah Eggleston, Rudi Pendavingh, Johannes Rau, and Chi Ho Yuen. The amoeba dimension of a linear space (2023). arXiv: 2303.13143.
Published
- [3]
-
Erwan Brugallé, Lucía López de Medrano, and Johannes Rau. Combinatorial patchworking: back from tropical geometry. Trans. Amer. Math. Soc. (accepted) (2022). arXiv: 2209.14043.
- [4]
-
Johannes Rau. Real semi-stable degenerations, real-oriented blow-ups and straightening corners. Int. Math. Res. Notices 2023.18 (2023), pp. 15896–15927. doi: 10.1093/imrn/rnad005. arXiv: 2203.17097.
- [5]
-
Johannes Rau, Arthur Renaudineau, and Kris Shaw. Real phase structures on matroid fans and matroid orientations. J. Lond. Math. Soc. 106.4 (2022), pp. 3687–3710. doi: 10.1112/jlms.12671. arXiv: 2106.08728.
- [6]
-
Johannes Rau. On the tropical Lefschetz-Hopf trace formula. J. Algebraic Combin. (2023). doi: 10.1007/s10801-023-01220-y. arXiv: 2010.07901.
- [7]
-
Johannes Rau. The tropical Poincaré-Hopf theorem. J. Combin. Theory Ser. A 196 (2023), p. 105733. doi: 10 . 1016 / j . jcta . 2023 . 105733. arXiv: 2007.11642.
- [8]
-
Grigory Mikhalkin and Johannes Rau. Spines for amoebas of rational curves. Enseign. Math. 65 (2 2019), pp. 377–396. doi: 10.4171/LEM/65-3/4-3. arXiv: 1906.04500.
- [9]
-
Jan Draisma, Johannes Rau, and Chi Ho Yuen. The dimension of an amoeba. Bull. London Math. Soc. 52.1 (2020), pp. 16–23. doi: 10.1112/blms.12301. arXiv: 1812.08149.
- [10]
-
Johannes Rau. Lower bounds and asymptotics of real double Hurwitz numbers. Math. Ann. 375.1-2 (2019), pp. 895–915. doi: 10.1007/s00208-019- 01863-y. arXiv: 1805.08997.
- [11]
-
Boulos El Hilany and Johannes Rau. Signed counts of real simple rational functions. J. Algebraic Combin. 52.3 (2020), pp. 369–403. doi: 10.1007/s10801- 019-00906-6. arXiv: 1712.05639.
- [12]
-
Philipp Jell, Johannes Rau, and Kristin Shaw. Lefschetz (1,1)-theorem in tropical geometry. Épijournal Géom. Algébrique 2.11 (2018). doi: 10. 46298/epiga.2018.volume2.4126. arXiv: 1711.07900.
- [13]
-
Ilia Itenberg, Grigory Mikhalkin, and Johannes Rau. Rational quintics in the real plane. Trans. Amer. Math. Soc. 370 (2018), pp. 131–196. doi: 10.1090/ tran/6938. arXiv: 1509.05228.
- [14]
-
Hannah Markwig and Johannes Rau. Tropical Real Hurwitz numbers. Math. Z. 281.1-2 (2015), pp. 501–522. doi: 10.1007/s00209- 015- 1498- 4. arXiv: 1412.4235.
- [15]
-
Mathieu Guay-Paquet, Hannah Markwig, and Johannes Rau. The Combinatorics of Real Double Hurwitz Numbers with Real Positive Branch Points. Int. Math. Res. Not. 2016.1 (2016), pp. 258–293. doi: 10. 1093/imrn/rnv135. arXiv: 1409.8095.
- [16]
-
Lars Allermann, Simon Hampe, and Johannes Rau. On rational equivalence in tropical geometry. Canad. J. Math. 68.2 (2016), pp. 241–257. doi: 10. 4153/CJM-2015-036-0. arXiv: 1408.1537.
- [17]
-
Georges François and Johannes Rau. The diagonal of tropical matroid varieties and cycle intersections. Collect. Math. 64.2 (2013), pp. 185–210. doi: 10.1007/s13348-012-0072-1. arXiv: 1012.3260.
- [18]
-
Johannes Rau. Intersections on tropical moduli spaces. Rocky Mt. J. Math. 46.2 (2016), pp. 581–662. doi: 10.1216/RMJ-2016-46-2-581. arXiv: 0812.3678.
- [19]
-
Hannah Markwig and Johannes Rau. Tropical descendant Gromov-Witten invariants. Manuscr. Math. 129.3 (2009), pp. 293–335. doi: 10.1007/s00229- 009-0256-5. arXiv: 0809.1102.
- [20]
-
Lars Allermann and Johannes Rau. First steps in tropical intersection theory. Math. Z. 264.3 (2010), pp. 633–670. doi: 10.1007/s00209-009-0483-1. arXiv: 0709.3705.
Others
- [21]
-
Johannes Rau. A First Expedition to Tropical Geometry. Lecture notes for a mini course given at the International School on Topological and Geometric Combinatorics, Tehran, Iran, 13–16/02/2017. 2018. url: https://math.uniandes.edu.co/~j.rau/downloads/FirstExpedition.pdf.
- [22]
-
Grigory Mikhalkin and Johannes Rau. Tropical Geometry. textbook in preparation. 2019. url: https://math.uniandes.edu.co/~j.rau/downloads/main.pdf.
- [23]
-
Boulos El Hilany, Johannes Rau, and Arthur Renaudineau. Combinatorial patchworking tool. Javascript applet. 2017. url: https://math.uniandes.edu.co/~j.rau/patchworking/patchworking.html.
- [24]
-
Johannes Rau. Tropical intersection theory and gravitational descendants. PhD-Thesis. Technische Universität Kaiserslautern, 2009. url: http://kluedo.ub.uni-kl.de/volltexte/2009/2370/.
Folien
- The dimension of amoebas
- Hilbert in the Tropics – Topology of real (nodal) curves
- Tropical Enumerative Geometry
- Tropical counts of real Hurwitz numbers (teilweise auf Deutsch)
- Polyeder – eine (T)Raumreise (Vortrag für Schulen/Öffentlichkeit)
Ausgewählte Vorträge
- 17/12/2019 MATRIX conference “Tropical geometry and mirror symmetry”, Creswick, Australia
- 01/10/2019 Workshop “Regensburg days on non-archimedean and tropical geometry”, Regensburg, Germany
- 13/09/2019 CMO Workshop “Tropical Methods in Real Algebraic Geometry”, Oaxaca, Mexico
- 29/04/2019 MFO-Workshop “Tropical Geometry: new directions”, Oberwolfach, Germany
- 22/01/2019 Seminar “Diskrete Mathematik/Geometrie”, TU Berlin, Germany
- 16/01/2019 Seminar “Topologie Algèbre et Géométrie”, Université de Nantes, France
- 03/12/2018 Colloquium talk, Universität Bern, Switzerland
- 02–04/05/2018 Lecture Series “Tropical methods in real algebraic geometry”, ASGARD math meeting, U Oslo, Norway
- 22/03/2018 Workshop on Moduli spaces of curves and mirror symmetry, IML Stockholm, Sweden
- 28/11/2017 Workshop “Young Researchers in String Mathematics”, MPI Bonn, Germany
- 13–16/02/2017 Lecture series “Tropical geometry”, School on Topological and Geometric Combinatorics, Tehran, Iran
- 11/01/2016 German-Israeli Workshop in Algebraic and Tropical Geometry, Tel Aviv, Israel
- 12/06/2015 AMS-EMS-SPM International Meeting, Session on Moduli Theory, Porto, Portugal
- 01/05/2015 MFO-Workshop “Tropical Aspects in Geometry, Topology and Physics”, Oberwolfach, Germany
- 18/09/2014 Meeting of the German and Polish mathematical societies, Real Algebraic Geometry workshop, Poznán, Poland
- 03/04/2013 Seminar “Géométrie tropicale”, Institut de Mathématiques de Jussieu, Paris, France
- 23/05/2011 Seminar “Géométrie symplectique”, Institut de Recherche Mathématique Avancée, Strasbourg, France
- 04/04/2008 Combinatorics seminar at the University of Michigan, Ann Arbor, USA
Organisation von Konferenzen
- 27–31/03/2017 Conference “Tropical curve counts, motivic integration and nonarchimedean geometry”, Universität Tübingen (joint with Hannah Markwig)
- 14–18/09/2015 Conference “Tropical Geometry in the Alps”, Les Diablerets, Switzerland (joint with Kristin Shaw, Grigory Mikhalkin)
- 24–28/11/2014 Closing conference of the TROPGEO project, Saas Fee, Switzerland (joint with Grigory Mikhalkin)
- 20/02/2013 Meeting of the seminar “Tropical Geometry in Europe”, Universität des Saarlandes (joint with Hannah Markwig)
- 17–20/09/2012 Minisymposium of the DMV annual meeting in Saarbrücken (joint with Hannah Markwig)
- 18–21/12/2011 Conference “Perspectives in Tropical Geometry 2011”, Arolla, Switzerland (joint with Grigory Mikhalkin)
Lehre
Vorlesungen
(Pro-)Seminare
Arbeitsgruppenseminare
|
|
Kontakt
|
j.rau (at) uniandes.edu.co Postanschrift
Departamento de Matemáticas |
Telefon
Fon: +57 1 3394949 Büro
Büro H-304 |


