Me and a blackboard

Johannes Rau

Departamento de Matemáticas
Facultad de Ciencias

Universidad de los Andes
Inicio Actual Investigación Publicaciones Docencia Contacto
Spanish English German
A tropical surface

Inicio

Soy profesor asociado en la Universidad de los Andes. Mi área de investigación es la geometría tropical y sus conexiones con la geometría enumerativa, la geometría algebraica real y la teoría de intersecciones. Mas generalmente, mi investigación está radicada en la geometría algebraica, la geometría simpléctica y la combinatoria. Si quieren saber más, miren abajo o escríbanme un mensaje.

Email: j.rau (at) uniandes.edu.co

Actual

MCA Session "Tropical Geometry, twistor spaces and cluster geometry"

Estoy organizando la sesión especial "Tropical Geometry, twistor spaces and cluster geometry" del Mathematical Congress of the Americas 2025 en Miami. Mis coorganizadores son Helge Ruddat, Lara Bossinger y Lucia Lopez de Medrano. Aquí puedes encontrar más información.

CETNAG poster

Colombian Encounter of Tropical and Non-archimedean Geometry

Junto con Pablo Cubides organicé la escuela y workshop "Colombian Encounter of Tropical and Non-archimedean Geometry". Este enlace te manda a la página web del evento.

LAGARTOS birthday poster

LAGARTOS

Hemos organizado quincenalmente el Latino-Americano Geometría Algebráica Real y Tropical Online Seminario (LAGARTOS).

Patchworking En Línea

Construya su curva algebraica personal con esta pequeña aplicación de browser.

Libro

Estoy preparando un libro sobre la geometría tropical en colaboración con Grigory Mikhalkin. El siguiente enlace lleva al borrador (más o menos) actual. Me alegraría mucho recibir sus correciones y sugerencias.

Investigación

Keywords

A real amoeba Mi area de investigación es la geometría tropical (el adjetivo pomposo tropical fue usado originalmente en el contexto del álgebra max-plus para honorar trabajo pionero del matemático brasilero (de decendencia hungariana) Imre Simon). Aunque los orígenes del area son más antiguos, la geometría tropical surgió como una nueva tendencia en la geometría algebraica y simpléctica alrededor del año 2000. Aquí hay una lista de palabras clave que describen mis intereses investigativos.

  1. Geometría enumerativa real
    • Números de Hurwitz reales
    • Invariantes descendientes de Gromov-Witten, Clases de Psi
  2. Topología de variedades algebraicas reales
    • Problema 16 de Hilbert para curvas nodales
    • Superficies algebraicas reales
  3. Teoría de intersección y de Hodge
    • Productos de intersección tropicales
    • Matroides
    • Grupos de Hodge tropicales
    • Equivalencia racional
  4. Libro
    Estoy preparando un libro sobre la geometría tropical en colaboración con Grigory Mikhalkin. El siguiente enlace lleva al borrador (más o menos) actual. Me alegraría mucho recibir sus correciones y sugerencias.
    Tropical geometry (Borrador, inglés)

Dinosaurs and skeletons

Tropical geometry for non-mathematicians

(hasta ahora, solo en inglés)

Tropical mathematics can be compared to the world of dinosaurs. When paleontologists want to learn more about these animals, they can't just go watch them in the zoo or the jungle, because unfortunately the poor things became extinct a long time ago. Instead, they work more like A tropical surface archeologists. They go digging for their bones, try to reassemble their skeletons, and from that draw conclusions about how these animals looked like, what they ate, how they hunted etc. In tropical geometry, we do exactly the same!

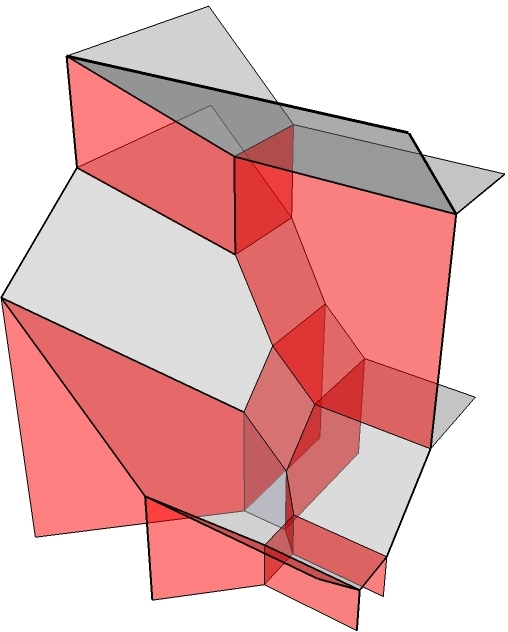
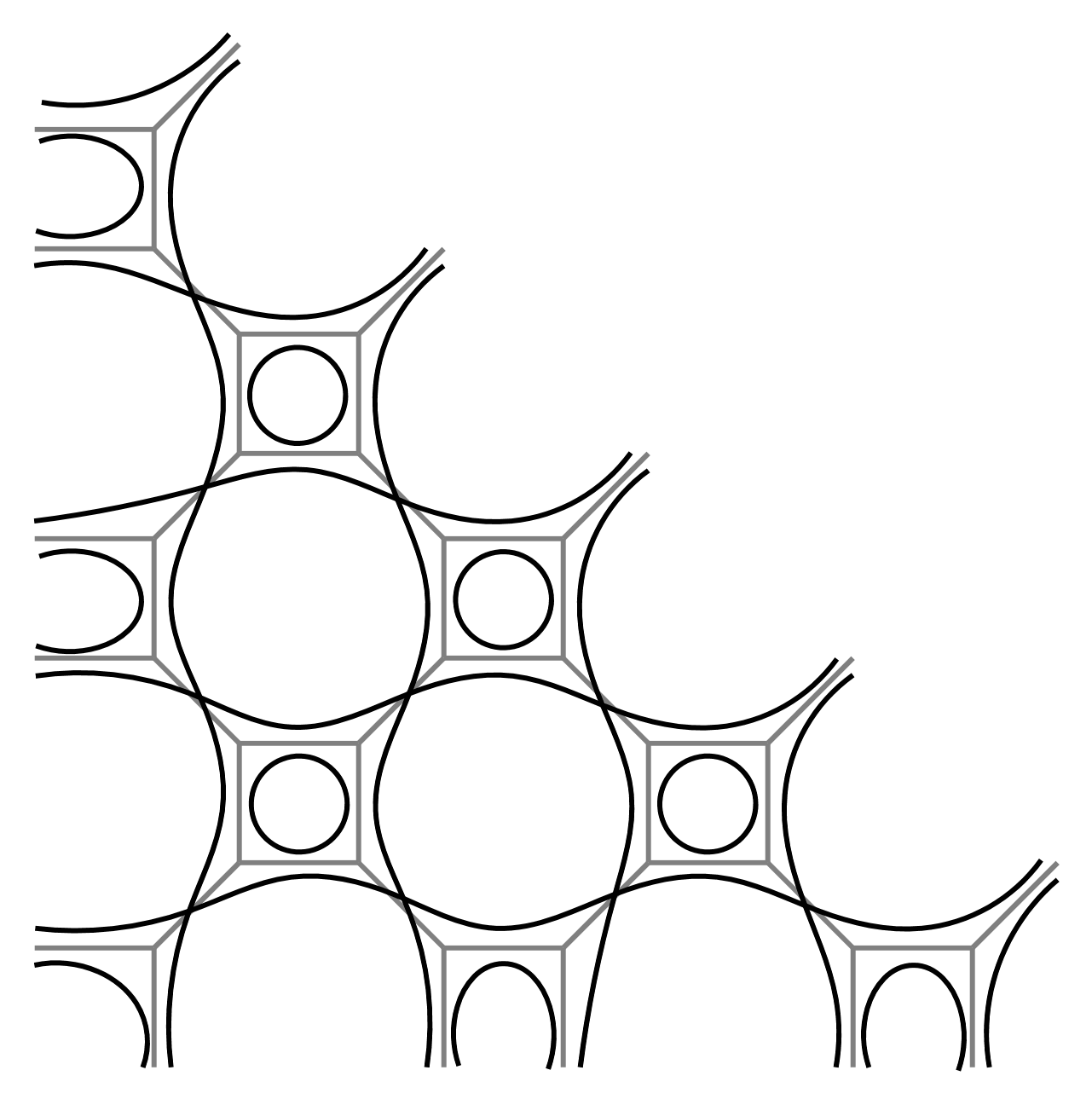
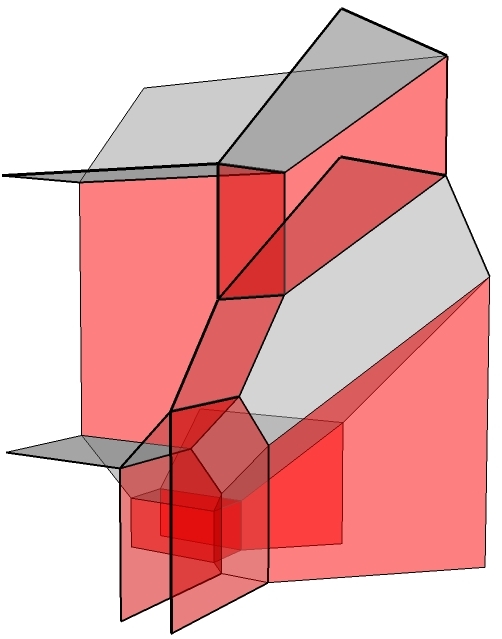
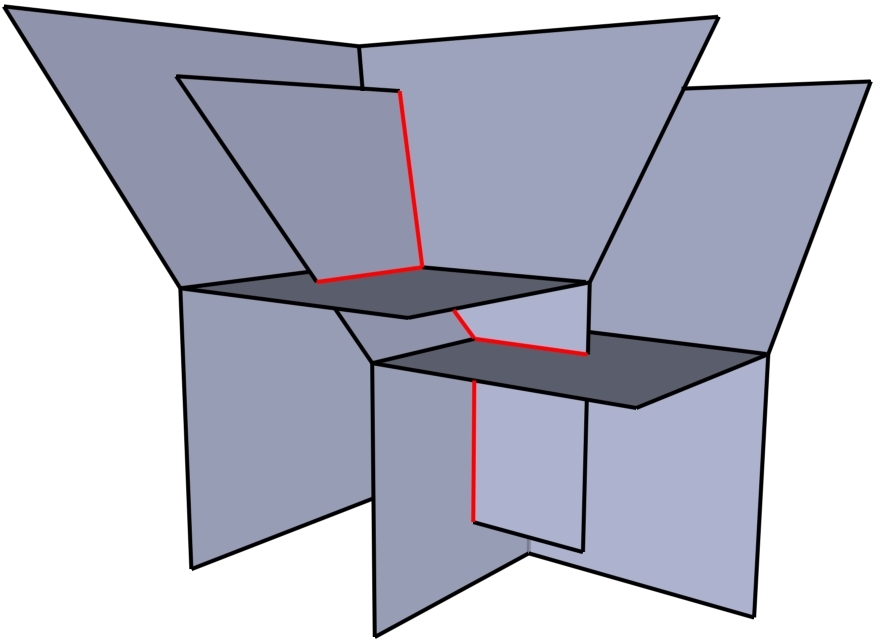
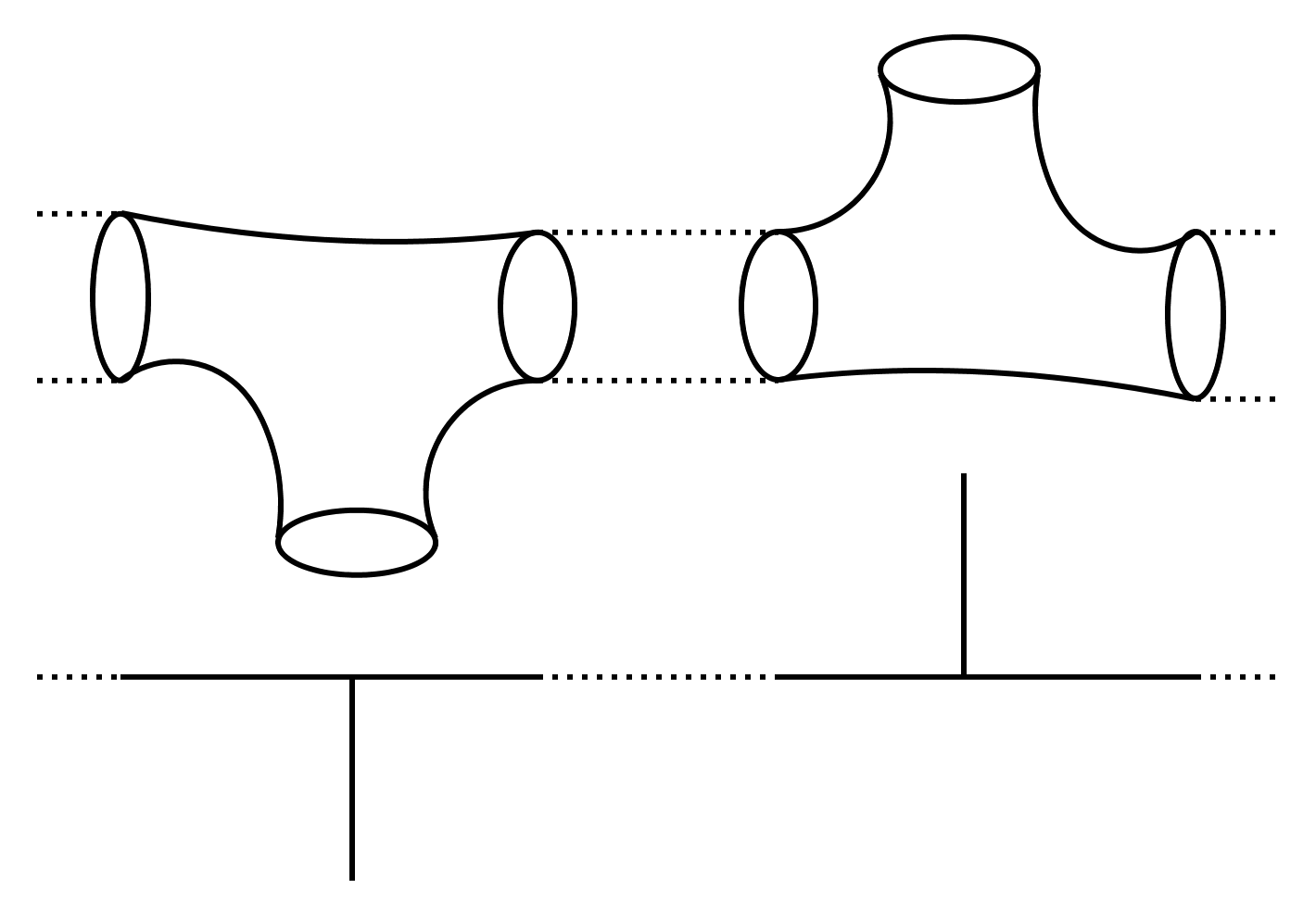
In our setting, the dinosaurs are called algebraic varieties. These are complicated geometrical shapes given by polynomial equations. Algebraic varieties show up all the time in mathematics, science and real life, and therefore their study forms one of the oldest and most sophisticated fields in mathematics (called algebraic geometry). Algebraic varieties are often so complicated that it is impossible to get our hands on them directly – like the extinct dinosaurs. However, in some cases mathematicians found a way to dig out the skeletons of these mathematical dinosaurs. Technically, you first have to turn the dinosaurs into amoebas and then starve them out until only their skeletons are left ;).

The mathematical skeletons are called tropical varieties, and in tropical geometry we play paleontologist and try to find out more about the original geometrical objects by studying their tropical skeletons (you can find some pictures on this page). The nice thing is that tropical varieties are much simpler objects than the original ones and can be studied in much more down-to-earh terms. Of course, we cannot work wonders and find answer to all questions (it is easy to estimate the size of the real-life dinosaur from its skeleton, but did it have furry or smooth skin?), but by now some remarkable facts about algebraic varieties were deduced from the study of their tropical skeletons, and that is why tropical geometry is at the moment such an exciting and steadily growing field.

Further Resources

Tropical geometry for students/mathematicians from other fields

You are bachelor/master student in mathematics (or a researcher from a different field) and want to embark on a first expedition to the tropics? Then have a look at these lecture notes.

These notes grew out of a lecture series I gave for bachelor students without any prior knowlwedge of the topic. They are therefore on a very elementary level and give priority to intution and illustrations as opposed to rigour and depth.

A combinatorial patchworking of degree 30

Presentations

A few slides with more info on some projects.

Combinatorial Patchworking

One of the origins of tropical geometry is Viro's patchworking method. The link below leads to a small browser app which allows you to do some experiments with this method.

You can use it to create your own real algebraic curves and pictures like the one to the right. It shows the (topological) shape of a planar real algebraic curve of degree 30 (that is, the set of zeros of a polynomial of degree 30 in the variables x and y). You can find some information on this topic in the following slides.

Publicaciones

Two planes intersect in a line

Artículos

Preprints

[1]

Johannes Rau, Arthur Renaudineau, and Kris Shaw. Real phase structures on tropical manifolds and patchworks in higher codimension. Preprint (2023). arXiv: 2310.08313.

[2]

Jan Draisma, Sarah Eggleston, Rudi Pendavingh, Johannes Rau, and Chi Ho Yuen. The amoeba dimension of a linear space (2023). arXiv: 2303.13143.

Published

[3]

Erwan Brugallé, Lucía López de Medrano, and Johannes Rau. Combinatorial patchworking: back from tropical geometry. Trans. Amer. Math. Soc. (accepted) (2022). arXiv: 2209.14043.

[4]

Johannes Rau. Real semi-stable degenerations, real-oriented blow-ups and straightening corners. Int. Math. Res. Notices 2023.18 (2023), pp. 15896–15927. doi: 10.1093/imrn/rnad005. arXiv: 2203.17097.

[5]

Johannes Rau, Arthur Renaudineau, and Kris Shaw. Real phase structures on matroid fans and matroid orientations. J. Lond. Math. Soc. 106.4 (2022), pp. 3687–3710. doi: 10.1112/jlms.12671. arXiv: 2106.08728.

[6]

Johannes Rau. On the tropical Lefschetz-Hopf trace formula. J. Algebraic Combin. (2023). doi: 10.1007/s10801-023-01220-y. arXiv: 2010.07901.

[7]

Johannes Rau. The tropical Poincaré-Hopf theorem. J. Combin. Theory Ser. A 196 (2023), p. 105733. doi: 10 . 1016 / j . jcta . 2023 . 105733. arXiv: 2007.11642.

[8]

Grigory Mikhalkin and Johannes Rau. Spines for amoebas of rational curves. Enseign. Math. 65 (2 2019), pp. 377–396. doi: 10.4171/LEM/65-3/4-3. arXiv: 1906.04500.

[9]

Jan Draisma, Johannes Rau, and Chi Ho Yuen. The dimension of an amoeba. Bull. London Math. Soc. 52.1 (2020), pp. 16–23. doi: 10.1112/blms.12301. arXiv: 1812.08149.

[10]

Johannes Rau. Lower bounds and asymptotics of real double Hurwitz numbers. Math. Ann. 375.1-2 (2019), pp. 895–915. doi: 10.1007/s00208-019- 01863-y. arXiv: 1805.08997.

[11]

Boulos El Hilany and Johannes Rau. Signed counts of real simple rational functions. J. Algebraic Combin. 52.3 (2020), pp. 369–403. doi: 10.1007/s10801- 019-00906-6. arXiv: 1712.05639.

[12]

Philipp Jell, Johannes Rau, and Kristin Shaw. Lefschetz (1,1)-theorem in tropical geometry. Épijournal Géom. Algébrique 2.11 (2018). doi: 10. 46298/epiga.2018.volume2.4126. arXiv: 1711.07900.

[13]

Ilia Itenberg, Grigory Mikhalkin, and Johannes Rau. Rational quintics in the real plane. Trans. Amer. Math. Soc. 370 (2018), pp. 131–196. doi: 10.1090/ tran/6938. arXiv: 1509.05228.

[14]

Hannah Markwig and Johannes Rau. Tropical Real Hurwitz numbers. Math. Z. 281.1-2 (2015), pp. 501–522. doi: 10.1007/s00209- 015- 1498- 4. arXiv: 1412.4235.

[15]

Mathieu Guay-Paquet, Hannah Markwig, and Johannes Rau. The Combinatorics of Real Double Hurwitz Numbers with Real Positive Branch Points. Int. Math. Res. Not. 2016.1 (2016), pp. 258–293. doi: 10. 1093/imrn/rnv135. arXiv: 1409.8095.

[16]

Lars Allermann, Simon Hampe, and Johannes Rau. On rational equivalence in tropical geometry. Canad. J. Math. 68.2 (2016), pp. 241–257. doi: 10. 4153/CJM-2015-036-0. arXiv: 1408.1537.

[17]

Georges François and Johannes Rau. The diagonal of tropical matroid varieties and cycle intersections. Collect. Math. 64.2 (2013), pp. 185–210. doi: 10.1007/s13348-012-0072-1. arXiv: 1012.3260.

[18]

Johannes Rau. Intersections on tropical moduli spaces. Rocky Mt. J. Math. 46.2 (2016), pp. 581–662. doi: 10.1216/RMJ-2016-46-2-581. arXiv: 0812.3678.

[19]

Hannah Markwig and Johannes Rau. Tropical descendant Gromov-Witten invariants. Manuscr. Math. 129.3 (2009), pp. 293–335. doi: 10.1007/s00229- 009-0256-5. arXiv: 0809.1102.

[20]

Lars Allermann and Johannes Rau. First steps in tropical intersection theory. Math. Z. 264.3 (2010), pp. 633–670. doi: 10.1007/s00209-009-0483-1. arXiv: 0709.3705.

Others

[21]

Johannes Rau. A First Expedition to Tropical Geometry. Lecture notes for a mini course given at the International School on Topological and Geometric Combinatorics, Tehran, Iran, 13–16/02/2017. 2018. url: https://math.uniandes.edu.co/~j.rau/downloads/FirstExpedition.pdf.

[22]

Grigory Mikhalkin and Johannes Rau. Tropical Geometry. textbook in preparation. 2019. url: https://math.uniandes.edu.co/~j.rau/downloads/main.pdf.

[23]

Boulos El Hilany, Johannes Rau, and Arthur Renaudineau. Combinatorial patchworking tool. Javascript applet. 2017. url: https://math.uniandes.edu.co/~j.rau/patchworking/patchworking.html.

[24]

Johannes Rau. Tropical intersection theory and gravitational descendants. PhD-Thesis. Technische Universität Kaiserslautern, 2009. url: http://kluedo.ub.uni-kl.de/volltexte/2009/2370/.

Presentaciones

Charlas seleccionadas

  • 17/12/2019 MATRIX conference “Tropical geometry and mirror symmetry”, Creswick, Australia
  • 01/10/2019 Workshop “Regensburg days on non-archimedean and tropical geometry”, Regensburg, Germany
  • 13/09/2019 CMO Workshop “Tropical Methods in Real Algebraic Geometry”, Oaxaca, Mexico
  • 29/04/2019 MFO-Workshop “Tropical Geometry: new directions”, Oberwolfach, Germany
  • 22/01/2019 Seminar “Diskrete Mathematik/Geometrie”, TU Berlin, Germany
  • 16/01/2019 Seminar “Topologie Algèbre et Géométrie”, Université de Nantes, France
  • 03/12/2018 Colloquium talk, Universität Bern, Switzerland
  • 02–04/05/2018 Lecture Series “Tropical methods in real algebraic geometry”, ASGARD math meeting, U Oslo, Norway
  • 22/03/2018 Workshop on Moduli spaces of curves and mirror symmetry, IML Stockholm, Sweden
  • 28/11/2017 Workshop “Young Researchers in String Mathematics”, MPI Bonn, Germany
  • 13–16/02/2017 Lecture series “Tropical geometry”, School on Topological and Geometric Combinatorics, Tehran, Iran
  • 11/01/2016 German-Israeli Workshop in Algebraic and Tropical Geometry, Tel Aviv, Israel
  • 12/06/2015 AMS-EMS-SPM International Meeting, Session on Moduli Theory, Porto, Portugal
  • 01/05/2015 MFO-Workshop “Tropical Aspects in Geometry, Topology and Physics”, Oberwolfach, Germany
  • 18/09/2014 Meeting of the German and Polish mathematical societies, Real Algebraic Geometry workshop, Poznán, Poland
  • 03/04/2013 Seminar “Géométrie tropicale”, Institut de Mathématiques de Jussieu, Paris, France
  • 23/05/2011 Seminar “Géométrie symplectique”, Institut de Recherche Mathématique Avancée, Strasbourg, France
  • 04/04/2008 Combinatorics seminar at the University of Michigan, Ann Arbor, USA

Organización de congresos

  • 27–31/03/2017 Conference “Tropical curve counts, motivic integration and nonarchimedean geometry”, Universität Tübingen (joint with Hannah Markwig)
  • 14–18/09/2015 Conference “Tropical Geometry in the Alps”, Les Diablerets, Switzerland (joint with Kristin Shaw, Grigory Mikhalkin)
  • 24–28/11/2014 Closing conference of the TROPGEO project, Saas Fee, Switzerland (joint with Grigory Mikhalkin)
  • 20/02/2013 Meeting of the seminar “Tropical Geometry in Europe”, Universität des Saarlandes (joint with Hannah Markwig)
  • 17–20/09/2012 Minisymposium of the DMV annual meeting in Saarbrücken (joint with Hannah Markwig)
  • 18–21/12/2011 Conference “Perspectives in Tropical Geometry 2011”, Arolla, Switzerland (joint with Grigory Mikhalkin)

Docencia

Cursos

2022-02 Geometría Algebraica
2022-02 Álgebra Lineal
2022-01 Álgebra Abstracta 1
2022-01 Álgebra Lineal
2021-02 Teoría de Hodge
2021-02 Cálculo Integral y Ecuaciones Diferenciales
2021-01 Variable Compleja
2021-01 Cálculo Integral y Ecuaciones Diferenciales
2020-02 Introducción a la Geometría Tropical
2020-02 Cálculo Integral y Ecuaciones Diferenciales
2020-01 Cálculo Integral y Ecuaciones Diferenciales
Invierno 19/20 Geometría Enumerativa Tropical 2
Verano 19 Análisis 1
Verano 19 Geometría Enumerativa Tropical 2
Invierno 18/19 Geometría Tropical
Verano 18 Geometría Algebraica I
Invierno 17/18 Algebra Lineal I
Invierno 17/18 Mate básica para Refugiados
Verano 17 Geometría Algebraica I
Verano 17 Mates básicas para Refugiados
Invierno 16/17 Teoría de Hodge Tropical
Verano 16 Curvas Algebraicas Reales
Invierno 15/16 Álgebra Lineal I
Verano 15 Algebra
Verano 14 Geometría Algebraica II
Invierno 13/14 Geometría Algebraica I
Verano 13 Álgebra
Invierno 12/13 Geometría Enumerativa

Seminarios de Estudiantes

2022-02 Teoría de Hodge de Matroides
Verano 16 De la Geometría Hiperbólica a la Teoría de nudos

Seminarios de Investigación

2020-01 Matroides y Geometría Tropical
Verano 17 Recursion Topológica
Invierno 16/17 Recursion Topológica
Verano 16 Integrable systems and tropical geometry
Invierno 15/16 Moduli spaces of log-stable maps
Verano 15 Cluster algebras
Verano 14 Derived Categories
Invierno 13/14 Random matrices and Hurwitz numbers
Verano 13 Moduli stacks of algebraic curves
Invierno 12/13 Berkovich spaces
A real nodal quartic

Contacto

Gluing pairs of pants

Correo electrónico

j.rau (at) uniandes.edu.co

Correo ordinario

Departamento de Matemáticas
Universidad de los Andes
Carrera 1 # 18A - 12
Bogotá, Colombia
Postal Code: 111711

Teléfono

Fon: +57 1 3394949
Ext: 2722

Oficina

Oficina H-304
Edificio H
Cómo llegar